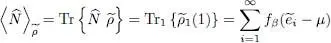(33) 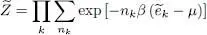
We simply get an expression similar to relation (7)of Complement B XV, obtained for an ideal gas. Since for fermions nk can only take the values 0 and 1, we get:
(34) 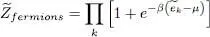
whereas for bosons nk varies from 0 to infinity, so that:
(35) 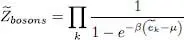
In both cases we can write:
(36) 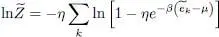
with η = +1 for bosons, and η = – 1 for fermions.
Computing the entropy can be done in a similar way. As the density operator 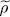 has the same form as the one describing the thermal equilibrium of an ideal gas, we can use for a system described by
has the same form as the one describing the thermal equilibrium of an ideal gas, we can use for a system described by 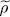 the formulas obtained for the entropy of a system without interactions.
the formulas obtained for the entropy of a system without interactions.
β. One particle, reduced density operator
Let us compute the average value of 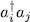 with the density operator
with the density operator 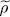 :
:
(37) 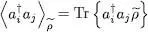
We saw in § 2-c of Complement B XVthat:
(38) 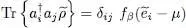
where the distribution function fβ is noted 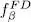 for fermions, and
for fermions, and 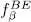 for bosons:
for bosons:
(39) 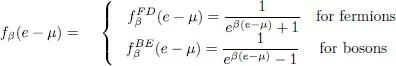
When the system is described by the density operator 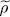 the average populations of the individual states
the average populations of the individual states 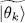 are therefore determined by the usual Fermi-Dirac or Bose-Einstein distributions. From now on, and to simplify the notation, we shall write simply | θk 〉 for the kets
are therefore determined by the usual Fermi-Dirac or Bose-Einstein distributions. From now on, and to simplify the notation, we shall write simply | θk 〉 for the kets 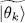 .
.
We can introduce a “one-particle reduced density operator” 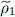 (1) by 2 :
(1) by 2 :
(40) 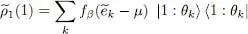
where the 1 enclosed in parentheses and the subscript 1 on the left-hand side emphasize we are dealing with an operator acting in the one-particle state space (as opposed to 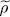 that acts in the Fock space); needless to say, this subscript has nothing to do with the initial numbering of the particles, but simply refers to any single particle among all the system particles. The diagonal elements of
that acts in the Fock space); needless to say, this subscript has nothing to do with the initial numbering of the particles, but simply refers to any single particle among all the system particles. The diagonal elements of 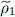 (1) are the individual state populations. With this operator, we can compute the average value over
(1) are the individual state populations. With this operator, we can compute the average value over 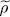 of any one-particle operator
of any one-particle operator 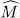 :
:
(41) 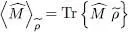
as we now show. Using the expression (B-12) of Chapter XVfor any one-particle operator 3 , as well as (38), we can write:
(42) 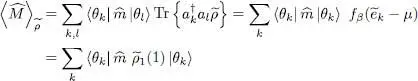
that is:
(43) 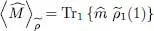
As we shall see, the density operator 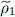 (1) is quite useful since it allows obtaining in a simple way all the average values that come into play in the Hartree-Fock computations. Our variational calculations will simply amount to varying
(1) is quite useful since it allows obtaining in a simple way all the average values that come into play in the Hartree-Fock computations. Our variational calculations will simply amount to varying 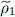 (1). This operator presents, in a certain sense, all the properties of the variational density operator
(1). This operator presents, in a certain sense, all the properties of the variational density operator 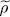 chosen in (28)in the Fock space. It plays the same role 4 as the projector PN (which also represents the essence of the variational N -particle ket) played in Complement E XV. In a general way, one can say that the basic principle of the Hartree-Fock method is to reduce the binary correlation functions of the system to products of single-particle correlation functions (more details on this point will be given in § 2-b of Complement C XVI).
chosen in (28)in the Fock space. It plays the same role 4 as the projector PN (which also represents the essence of the variational N -particle ket) played in Complement E XV. In a general way, one can say that the basic principle of the Hartree-Fock method is to reduce the binary correlation functions of the system to products of single-particle correlation functions (more details on this point will be given in § 2-b of Complement C XVI).
The average value of the operator 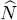 for the total particle number is written:
for the total particle number is written:
(44) 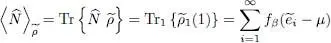
Читать дальше

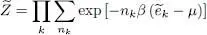
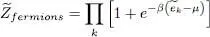
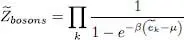
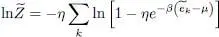
 has the same form as the one describing the thermal equilibrium of an ideal gas, we can use for a system described by
has the same form as the one describing the thermal equilibrium of an ideal gas, we can use for a system described by 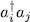 with the density operator
with the density operator 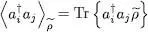
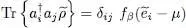
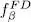 for fermions, and
for fermions, and 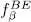 for bosons:
for bosons: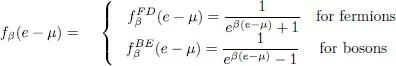
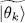 are therefore determined by the usual Fermi-Dirac or Bose-Einstein distributions. From now on, and to simplify the notation, we shall write simply | θk 〉 for the kets
are therefore determined by the usual Fermi-Dirac or Bose-Einstein distributions. From now on, and to simplify the notation, we shall write simply | θk 〉 for the kets 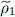 (1) by 2 :
(1) by 2 :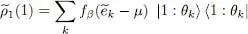
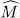 :
: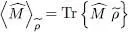
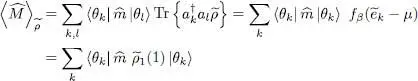
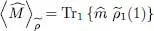
 for the total particle number is written:
for the total particle number is written: