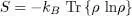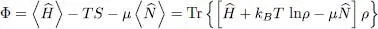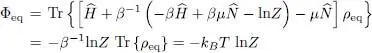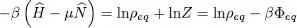Because of the particle interactions, these formulas generally lead to calculations too complex to be carried to completion. We therefore look, in this complement, for approximate expressions of ρ eqand Z that are easier to use and are based on the mean field approximation.
Consider two density operators ρ and ρ′ , both having a trace equal to 1:
(7) 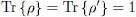
As we now show, the following relation is always true:
(8) 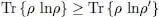
We first note that the function x ln x , defined for x ≥ 0, is always larger than the function x – 1, which is the equation of its tangent at x = 1 ( Fig. 1). For positive values of x and y we therefore always have:
(9) 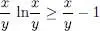
or, after multiplying by y :
(10) 
the equality occurring only if x = y .
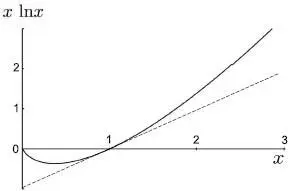
Figure 1: Plot of the function x lnx. At x = 1 , this curve is tangent to the line y = x – 1 (dashed line) but always remains above it; the function value is thus always larger than x – 1.
Let us call pn the eigenvalues of ρ corresponding to the normalized eigenvectors | un 〉, and  the eigenvalues of ρ′ corresponding to the normalized eigenvectors | vm 〉. Used for the positive numbers pn and
the eigenvalues of ρ′ corresponding to the normalized eigenvectors | vm 〉. Used for the positive numbers pn and  , relation (10)yields:
, relation (10)yields:
(11) 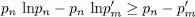
We now multiply this relation by the square of the modulus of the scalar product:
(12) 
and sum over m and n . For the term in pn ln pn of (11), the summation over m yields in (12)the identity operator expanded on the basis {| v m〉}; we then get 〈 un | un 〉 = 1, and are left with the sum over n of pn ln pn , that is the trace Tr{ ρ ln ρ }. As for the term in pn ln  , the summation over m introduces:
, the summation over m introduces:
(13) 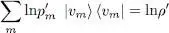
and we get:
(14) 
As for the terms on the right-hand side of inequality (11), the term in pn yields:
(15) 
and the one in  also yields 1 for the same reasons, and both terms cancel out. We finally obtain the inequality:
also yields 1 for the same reasons, and both terms cancel out. We finally obtain the inequality:
(16) 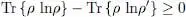
which proves (8).
Comment:
One may wonder under which conditions the above relation becomes an equality. This requires the inequality (11)to become an equality, which means  whenever the scalar product (12)is non-zero; consequently all the eigenvalues of the two operators ρ and ρ′ must be equal. In addition, the eigenvectors of each operator corresponding to different eigenvalues must be orthogonal (their scalar product must be zero). In other words, the eigenvalues and the subspaces spanned by their eigenvectors are identical, which amounts to saying that ρ = ρ′ .
whenever the scalar product (12)is non-zero; consequently all the eigenvalues of the two operators ρ and ρ′ must be equal. In addition, the eigenvectors of each operator corresponding to different eigenvalues must be orthogonal (their scalar product must be zero). In other words, the eigenvalues and the subspaces spanned by their eigenvectors are identical, which amounts to saying that ρ = ρ′ .
1-c. Minimization of the thermodynamic potential
The entropy S associated with any density operator ρ having a trace equal to 1 is defined by relation (6)of Appendix VI:
(17) 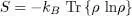
The thermodynamic potential of the grand canonical ensemble is defined by the “grand potential” Φ, which can be expressed as a function of ρ by relation ( Appendix VI, § 1-c- β ):
(18) 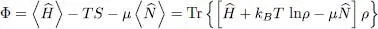
Inserting (5)into (18), we see that the value of Φ at equilibrium, Φ eq, can be directly obtained from the partition function Z :
(19) 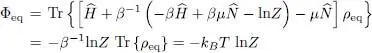
We therefore have:
(20) 
Consider now any density operator ρ and its associated function Φ obtained from (18). According to (5)and (20), we can write:
(21) 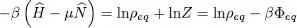
Inserting this result in (18)yields:
(22) 
Now relation (16), used with ρ′ = ρ eq, is written as:
Читать дальше

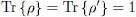
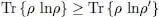
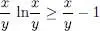


 the eigenvalues of ρ′ corresponding to the normalized eigenvectors | vm 〉. Used for the positive numbers pn and
the eigenvalues of ρ′ corresponding to the normalized eigenvectors | vm 〉. Used for the positive numbers pn and 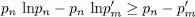

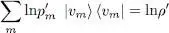


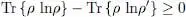
 whenever the scalar product (12)is non-zero; consequently all the eigenvalues of the two operators ρ and ρ′ must be equal. In addition, the eigenvectors of each operator corresponding to different eigenvalues must be orthogonal (their scalar product must be zero). In other words, the eigenvalues and the subspaces spanned by their eigenvectors are identical, which amounts to saying that ρ = ρ′ .
whenever the scalar product (12)is non-zero; consequently all the eigenvalues of the two operators ρ and ρ′ must be equal. In addition, the eigenvectors of each operator corresponding to different eigenvalues must be orthogonal (their scalar product must be zero). In other words, the eigenvalues and the subspaces spanned by their eigenvectors are identical, which amounts to saying that ρ = ρ′ .