(78) 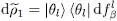
and thus leads to variations of expressions (61)of 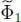 and
and  . Their sum is:
. Their sum is:
(79) 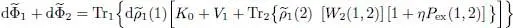
where the factor 1/2 in  has been canceled since the variations induced by
has been canceled since the variations induced by 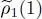 and
and 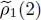 double each other. Inserting (78)in this relation and using again (74), we get:
double each other. Inserting (78)in this relation and using again (74), we get:
(80) 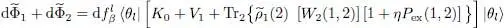
As for 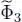 , its variation is the sum of a term in
, its variation is the sum of a term in 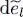 coming from the explicit presence of the energies
coming from the explicit presence of the energies 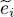 in its definition (61), and a term in
in its definition (61), and a term in 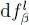 . If we let only the energy
. If we let only the energy 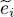 vary (not taking into account the variations of the distribution function), we get a zero result, since:
vary (not taking into account the variations of the distribution function), we get a zero result, since:
(81) 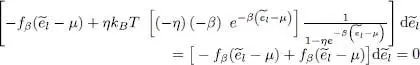
Consequently, we just have to vary by 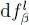 the distribution function, and we get:
the distribution function, and we get:
(82) 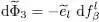
Finally, after simplification by 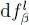 (which, by hypothesis, is different from zero), imposing the variation
(which, by hypothesis, is different from zero), imposing the variation 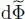 to be zero leads to the condition:
to be zero leads to the condition:
(83) 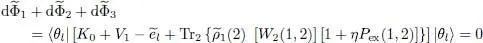
This expression does look like the stationarity condition at constant energy (77), but now the subscripts l and m are the same, and a term in 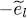 is present in the operator.
is present in the operator.
3. Temperature dependent mean field equations
Introducing a Hartree-Fock operator acting in the single particle state space allows writing the stationarity relations just obtained in a more concise and manageable form, as we now show.
3-a. Form of the equations
Let us define a temperature dependent Hartree-Fock operator as the partial trace that appears in the previous equations:
(84) 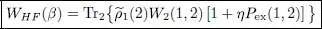
It is thus an operator acting on the single particle 1. It can be defined just as well by its matrix elements between the individual states:
(85) 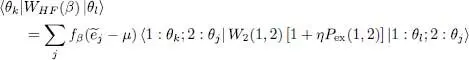
Equation (77)is valid for any two chosen values l and m , as long as 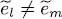 . When l is fixed and m varies, it simply means that the ket:
. When l is fixed and m varies, it simply means that the ket:
(86) 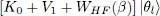
is orthogonal to all the eigenvectors | θm 〉 having an eigenvalue 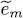 different from
different from 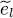 ; it has a zero component on each of these vectors. As for equation (83), it yields the component of this ket on | θl 〉, which is equal to
; it has a zero component on each of these vectors. As for equation (83), it yields the component of this ket on | θl 〉, which is equal to 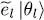 . The set of | θm 〉 (including those having the same eigenvalue as | θl 〉) form a basis of the individual state space, defined by (26)as the basis of eigenvectors of the individual operator
. The set of | θm 〉 (including those having the same eigenvalue as | θl 〉) form a basis of the individual state space, defined by (26)as the basis of eigenvectors of the individual operator 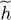 . Two cases must be distinguished:
. Two cases must be distinguished:
(i) If 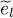 is a non-degenerate eigenvalue of
is a non-degenerate eigenvalue of 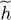 , the set of equations (77)and (83)determine all the components of the ket [ K0 + V 1+ WHF ( β )]| θl 〉). This shows that | θl 〉 is an eigenvector of the operator K 0+ V 1+ WHF with the eigenvalue
, the set of equations (77)and (83)determine all the components of the ket [ K0 + V 1+ WHF ( β )]| θl 〉). This shows that | θl 〉 is an eigenvector of the operator K 0+ V 1+ WHF with the eigenvalue 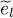 .
.
(ii) If this eigenvalue of 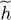 is degenerate, relation (77)only proves that the eigen-subspace of
is degenerate, relation (77)only proves that the eigen-subspace of 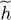 , with eigenvalue
, with eigenvalue 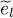 , is stable under the action of the operator K 0+ V 1+ WHF it does not yield any information on the components of the ket (86)inside that subspace. It is possible though to diagonalize K 0+ V 1+ WHF inside each of the eigen-subspace of
, is stable under the action of the operator K 0+ V 1+ WHF it does not yield any information on the components of the ket (86)inside that subspace. It is possible though to diagonalize K 0+ V 1+ WHF inside each of the eigen-subspace of 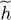 , which leads to a new eigenvectors basis | φn 〉, now common to
, which leads to a new eigenvectors basis | φn 〉, now common to 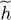 and K 0+ V 1+ WHF .
and K 0+ V 1+ WHF .
Читать дальше

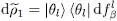
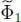 and
and  . Their sum is:
. Their sum is: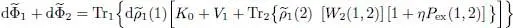
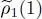 and
and 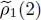 double each other. Inserting (78)in this relation and using again (74), we get:
double each other. Inserting (78)in this relation and using again (74), we get: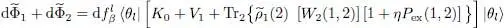
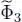 , its variation is the sum of a term in
, its variation is the sum of a term in 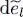 coming from the explicit presence of the energies
coming from the explicit presence of the energies 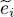 in its definition (61), and a term in
in its definition (61), and a term in 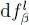 . If we let only the energy
. If we let only the energy 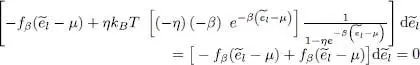
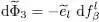
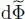 to be zero leads to the condition:
to be zero leads to the condition: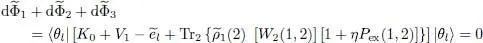
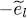 is present in the operator.
is present in the operator.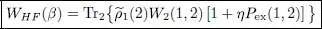
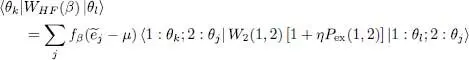
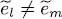 . When l is fixed and m varies, it simply means that the ket:
. When l is fixed and m varies, it simply means that the ket: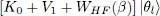
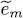 different from
different from 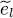 ; it has a zero component on each of these vectors. As for equation (83), it yields the component of this ket on | θl 〉, which is equal to
; it has a zero component on each of these vectors. As for equation (83), it yields the component of this ket on | θl 〉, which is equal to 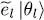 . The set of | θm 〉 (including those having the same eigenvalue as | θl 〉) form a basis of the individual state space, defined by (26)as the basis of eigenvectors of the individual operator
. The set of | θm 〉 (including those having the same eigenvalue as | θl 〉) form a basis of the individual state space, defined by (26)as the basis of eigenvectors of the individual operator 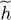 . Two cases must be distinguished:
. Two cases must be distinguished: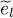 is a non-degenerate eigenvalue of
is a non-degenerate eigenvalue of 










