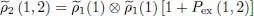We now reason in this new basis where all the [ K 0+ V 1+ WHF ( β )]| φn 〉 are proportional to | φn 〉. Taking (83)into account, we get:
(87) 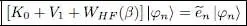
As we just saw, the basis change from the | θl 〉 to the | φn 〉 only occurs within the eigen-subspaces of 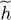 corresponding to given eigenvalues
corresponding to given eigenvalues 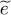 ; one can then replace the | θl 〉 by the | φn 〉 in the definition (40)of
; one can then replace the | θl 〉 by the | φn 〉 in the definition (40)of 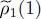 and write:
and write:
(88) 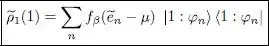
Inserting this relation in the definition (84)of WHF ( β ) leads to a set of equations only involving the eigenvectors | φn 〉.
For all the values of n we get a set of equations (87), which, associated with (84)and (88)defining the potential WHF ( β ) as a function of the | φn 〉, are called the temperature dependent Hartree-Fock equations.
3-b. Properties and limits of the equations
We now discuss how to apply the mean field equations we have obtained, and their limit of validity, which are more stringent for bosons than for fermions.
Hartree-Fock equations concern a self-consistent and nonlinear system: the eigenvectors | φn 〉 and eigenvalues of the density operator 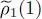 are solutions of an eigenvalue equation (87)which itself depends on
are solutions of an eigenvalue equation (87)which itself depends on 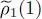 . This situation is reminiscent of the one encountered with the zero-temperature Hartree-Fock equations, and, a priori, no exact solutions can be found.
. This situation is reminiscent of the one encountered with the zero-temperature Hartree-Fock equations, and, a priori, no exact solutions can be found.
As for the zero-temperature case, we proceed by iteration: starting from a physically reasonable density operator 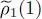 , we use it in (84)to compute a first value of the Hartree-Fock potential operator. We then diagonalize this operator to get its eigenkets and eigenvalues
, we use it in (84)to compute a first value of the Hartree-Fock potential operator. We then diagonalize this operator to get its eigenkets and eigenvalues 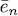 . Next, we build the operator
. Next, we build the operator 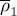 that has the same eigenkets, but whose eigenvalues are the
that has the same eigenkets, but whose eigenvalues are the 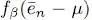 . Inserting this new operator
. Inserting this new operator 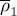 in (84), we get a second iteration of the Hartree-Fock operator. We again diagonalize this operator to compute new eigenvalues and eigenvectors, on which we build the next approximation
in (84), we get a second iteration of the Hartree-Fock operator. We again diagonalize this operator to compute new eigenvalues and eigenvectors, on which we build the next approximation 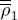 of
of 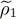 , and so on. After a few iterations, we may expect convergence towards a self-consistent solution.
, and so on. After a few iterations, we may expect convergence towards a self-consistent solution.
For a fermion system, there is no fundamental general limit for using the Hartree-Fock approximation. The pertinence of the final result obviously depends on the nature of the interactions, and whether a mean field treatment of these interactions is a good approximation. One can easily understand that the larger the interaction range, the more each particle will be submitted to the action of many others. This will lead to an averaging effect improving the mean field approximation. If, on the other hand, each particle only interacts with a single partner, strong binary correlations may appear, which cannot be correctly treated by a mean field acting on independent particles.
For bosons, the same general remarks apply, but the populations are no longer limited to 1 . When, for example, Bose-Einstein condensation occurs, one population becomes much larger than the others, and presents a singularity that is not accounted for in the calculations presented above. The Hartree-Fock approximation has therefore more severe limitations than for the fermions, and we now discuss this problem.
For a boson system in which many individual states have comparable populations, taking into account the interactions by the Hartree-Fock mean field yields as good an approximation as for a fermion system. If the system however is close to condensation, or already condensed, the mean field equations we have written are no longer valid. This is because the trial density operator in relation (31)contains a distribution function associated with each individual quantum state and varies as for an ideal gas, i.e. as an exponentially decreasing function of the occupation numbers. Now we saw in § 3-b- β of Complement B XVthat, in an ideal gas, the fluctuations of the particle numbers in each of the individual states are as large as the average values of those particle numbers. If the individual state has a large population, these fluctuations can become very important, which is physically impossible in the presence of repulsive interactions. Any population fluctuation increases the average value of the square of the occupation number (equal to the sum of the squared average value and the squared fluctuation), and hence of the interaction energy (proportional to the average value of the square). A large fluctuation in the populations would lead to an important increase of the interaction repulsive energy, in contradiction with the minimization of the thermodynamic potential. In other words, the finite compressibility of the physical system, introduced by the interactions, prevents any large fluctuation in the density. Consequently, the fluctuations in the number of condensed particles predicted by the trial Hartree-Fock density operator are not physically acceptable, in the presence of condensation.
It is worth analyzing more precisely the origin of this Hartree-Fock approximation limit, in terms of correlations between the particles. Relation (51)concerns any two-particle operator 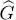 . It shows that, using the trial density operator (31), the two-particle reduced density operator can be written as:
. It shows that, using the trial density operator (31), the two-particle reduced density operator can be written as:
(89) 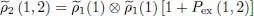
Читать дальше

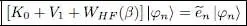
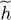 corresponding to given eigenvalues
corresponding to given eigenvalues 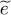 ; one can then replace the | θl 〉 by the | φn 〉 in the definition (40)of
; one can then replace the | θl 〉 by the | φn 〉 in the definition (40)of 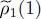 and write:
and write: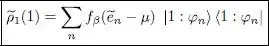
 are solutions of an eigenvalue equation (87)which itself depends on
are solutions of an eigenvalue equation (87)which itself depends on  . Next, we build the operator
. Next, we build the operator 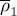 that has the same eigenkets, but whose eigenvalues are the
that has the same eigenkets, but whose eigenvalues are the 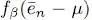 . Inserting this new operator
. Inserting this new operator 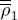 of
of 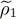 , and so on. After a few iterations, we may expect convergence towards a self-consistent solution.
, and so on. After a few iterations, we may expect convergence towards a self-consistent solution.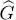 . It shows that, using the trial density operator (31), the two-particle reduced density operator can be written as:
. It shows that, using the trial density operator (31), the two-particle reduced density operator can be written as: