Let us introduce a general variational principle; using the stationarity of a functional S of the state vector Ψ( t )〉, it will yield the time-dependent Schrödinger equation.
2-a. Definition of a functional
Consider an arbitrarily given Hamiltonian H ( t ). We assume the state vector |Ψ( t )〉 to have any time dependence, and we note 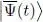 the ket physically equivalent to |Ψ( t )〉, but with a constant norm:
the ket physically equivalent to |Ψ( t )〉, but with a constant norm:
(6) 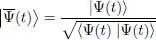
The functional S of 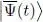 is defined as 1 :
is defined as 1 :
(7) 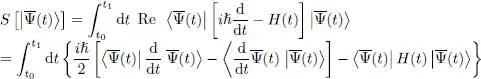
where t 0and t 1are two arbitrary times such that t 0< t 1. In the particular case where the chosen 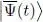 is equal to a solution
is equal to a solution 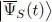 of the Schrödinger equation:
of the Schrödinger equation:
(8) 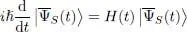
the bracket on the first line of (7)obviously cancels out and we have:
(9) 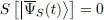
Integrating by parts the second term 2 of the bracket in the second line of (7), we get the same form as the first term in the bracket, plus an already integrated term. The final result is then:
(10) 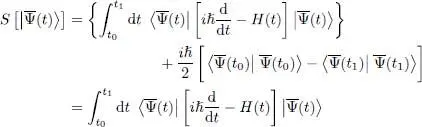
where we have used in the second line the fact that the norm of 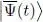 always remains equal to unity. This expression for S is similar to the initial form (7), but without the real part.
always remains equal to unity. This expression for S is similar to the initial form (7), but without the real part.
Suppose now 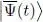 has an arbitrary time dependence between t 0and t 1, while keeping its norm constant, as imposed by (6); the functional then takes a certain value S , a priori different from zero. Let us see under which conditions S will be stationary when
has an arbitrary time dependence between t 0and t 1, while keeping its norm constant, as imposed by (6); the functional then takes a certain value S , a priori different from zero. Let us see under which conditions S will be stationary when 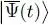 changes by an infinitely small amount
changes by an infinitely small amount 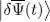 :
:
(11) 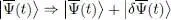
For what follows, it will be convenient to assume that the variation 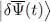 is free; we therefore have to ensure that the norm of
is free; we therefore have to ensure that the norm of 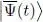 remains constant, equal to unity 3 . We introduce Lagrange multipliers (Appendix V) λ( t ) to control the square of the norm at every time between t 0and t 1, and we look for the stationarity of a function where the sum of constraints has been added. This sum introduces an integral, and we the function in question is:
remains constant, equal to unity 3 . We introduce Lagrange multipliers (Appendix V) λ( t ) to control the square of the norm at every time between t 0and t 1, and we look for the stationarity of a function where the sum of constraints has been added. This sum introduces an integral, and we the function in question is:
(12) 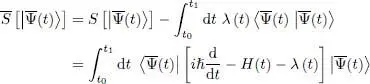
where λ( t ) is a real function of the time t .
The variation 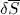 of
of 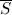 to first order is obtained by inserting (11)in (10). It yields the sum of a first term
to first order is obtained by inserting (11)in (10). It yields the sum of a first term 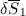 containing the ket
containing the ket 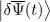 and of another
and of another 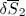 containing the bra
containing the bra 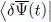 :
:
(13) 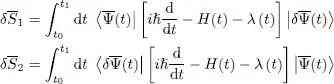
We now imagine another variation for the ket:
(14) 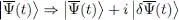
which yields a variation 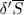 of
of 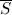 ; in this second variation, the term in
; in this second variation, the term in 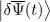 becomes
becomes 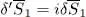 , whereas the term in
, whereas the term in 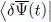 becomes
becomes 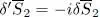 . Now, if the functional is stationary in the vicinity of
. Now, if the functional is stationary in the vicinity of 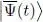 , the two variations
, the two variations 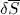 and
and 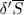 are necessarily zero, as are also
are necessarily zero, as are also 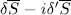 and
and 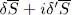 . In those combinations, only terms in
. In those combinations, only terms in 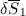 appear for the first one, and in
appear for the first one, and in 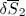 for the second; consequently they must both be zero. As a result, we can write the stationarity conditions with respect to variations of the bra and the ket separately.
for the second; consequently they must both be zero. As a result, we can write the stationarity conditions with respect to variations of the bra and the ket separately.
Читать дальше

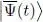 the ket physically equivalent to |Ψ( t )〉, but with a constant norm:
the ket physically equivalent to |Ψ( t )〉, but with a constant norm: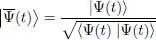
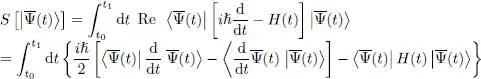
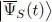 of the Schrödinger equation:
of the Schrödinger equation: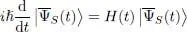
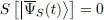
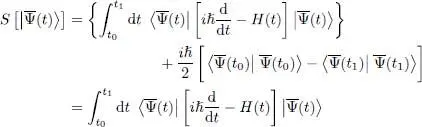
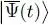 changes by an infinitely small amount
changes by an infinitely small amount 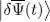 :
: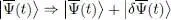
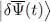 is free; we therefore have to ensure that the norm of
is free; we therefore have to ensure that the norm of 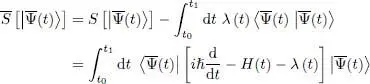
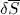 of
of 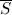 to first order is obtained by inserting (11)in (10). It yields the sum of a first term
to first order is obtained by inserting (11)in (10). It yields the sum of a first term 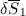 containing the ket
containing the ket 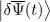 and of another
and of another 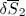 containing the bra
containing the bra 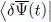 :
: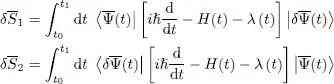
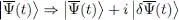
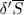 of
of 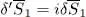 , whereas the term in
, whereas the term in 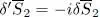 . Now, if the functional is stationary in the vicinity of
. Now, if the functional is stationary in the vicinity of 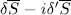 and
and 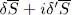 . In those combinations, only terms in
. In those combinations, only terms in 










