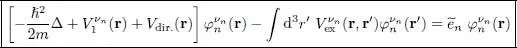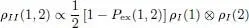with:
(92) 
This component of the mean field (Hartree term) contains a sum over all occupied states, whatever their spin is; it is spin independent.
(ii) We now turn to the exchange term, which contains the operator P ex(1,2) in the bracket of (87). To deal with it, we can for example commute in (87)the two operators W 2(1, 2) and P ex(1, 2); this last operator will then permute the two particles in the bra. Performing this operation in (90), we get, with the minus sign of the exchange term:
(93) 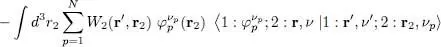
The scalar product will yield the products of δννp δνp ν′ δ ( r– r 2), making the integral over d 3 r 2disappear; this term is zero if ν ≠ ν ′, hence the factor δνν′ . Since W 2( r′, r) = W 2( r, r′), we are left with:
(94) 
where the sum is over the values of p for which νp = ν = ν ′ (hence, limited to the first N +values of p , or the last N –, depending on the case); the exchange potential 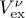 has been defined as:
has been defined as:
(95) 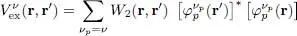
As is the case for the direct term, the exchange term does not act on the spin. There are however two differences. To begin with, the summation over p is limited to the states having the same spin v ; second, it introduces a contribution which is non-diagonal in the positions (but without an integral), and which cannot be reduced to an ordinary potential (the term “non-local potential” is sometimes used to emphasize this property).
We have shown that the scalar product of equation (77)with 〈 r, ν | introduces three potentials (in addition to the the one-body potential 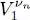 ), a direct potential V dir( r) and two exchange potentials
), a direct potential V dir( r) and two exchange potentials 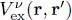 with ν = ±1/2. Equation (77)then becomes, in the {| r, ν 〉} representation, a pair of equations:
with ν = ±1/2. Equation (77)then becomes, in the {| r, ν 〉} representation, a pair of equations:
(96) 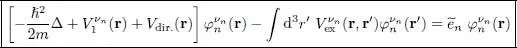
These are the Hartree-Fock equations with spin and in the position representation, widely used in quantum physics and chemistry. It is not necessary to worry, in these equations, about the term in which the subscript p in the summation appearing in (92)and (95)is the same as the subscript n (of the wave function we are looking for); the contributions n = p cancel each other exactly in the direct and exchange potentials.
Both the “Hartree term” giving the direct potential contribution, and the “Fock term “ giving the exchange potential, can be interpreted in the same way as above (§ 1-f). The Hartree term contains the contributions of all the other electrons to the mean potential felt by one electron. The exchange potential, on the other hand, only involves electrons in the same spin state, and this can be simply interpreted: the exchange effect only occurs for two totally indistinguishable particles. Now if these particles are in orthogonal spin states, and as the interactions do not act on the spins, one can in principle determine which is which and the particles become distinguishable: the quantum exchange effects cancel out. As we already pointed out, the exchange potential is not a potential stricto sensu. It is not diagonal in the position representation, even though it basically comes from a particle interaction that is diagonal in position. It is the antisymmetrization of the fermions, together with the chosen variational approximation, which led to this peculiar non-diagonal form. It is however a Hermitian operator, as can be shown using the fact that the initial potential W 2( r, r′) is real and symmetric with respect to rand r′.
The resolution of the nonlinear Hartree-Fock equations is generally done by the successive iteration approximate method discussed in § 1-f. There is no particular reason for the solution of the Hartree-Fock equations to be unique 8 ; on the contrary, they can yield solutions that depend on the states chosen to begin the nonlinear iterations. They can actually lead to a whole spectrum of possible energies for the system. This is how the ground state and excited state energies of the atom are generally computed. The atomic orbitals discussed in Complement E VII, the central field approximation and the electronic “configurations” discussed in Complement B XIVcan now be discussed in a more precise and quantitative way. We note that the exchange energy, introduced in this complement for a two-electron system, is a particular case of the exchange energy term of the Hartree-Fock potential. There exist however many other physical systems where the same ideas can be applied: nuclei (the Coulomb force is then replaced by the nuclear interaction force between the nucleons), atomic aggregates (with an interatomic potential having both repulsive and attractive components, see Complements C XIand G XI), and many others.
Once a Hartree-Fock solution for a complex problem has been found, we can go further. One can use the basis of the eigenfunctions just obtained as a starting point for more precise perturbation calculations, including for example correlations between particles (Chapter XI). In atomic spectra, we sometimes find cases where two configurations yield very close mean field energies. The effects of the interaction terms beyond the mean field approximation will then be more important. Perturbation calculations limited to the space of the configurations in question permits obtaining better approximations for the energy levels and their wave functions; one then speaks of “mixtures”, or of “interactions between configurations”.
Comment:
The variational method based on the Fock states is not the only one that leads to the Hartree-Fock equations. One could also start from an approximation of the two-particle density operator ρII by a function of the one-particle density operator ρI and write:
(97) 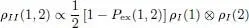
Читать дальше


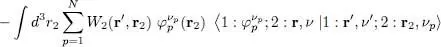

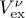 has been defined as:
has been defined as: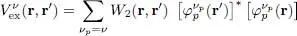
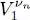 ), a direct potential V dir( r) and two exchange potentials
), a direct potential V dir( r) and two exchange potentials 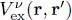 with ν = ±1/2. Equation (77)then becomes, in the {| r, ν 〉} representation, a pair of equations:
with ν = ±1/2. Equation (77)then becomes, in the {| r, ν 〉} representation, a pair of equations: