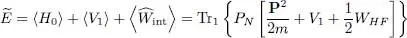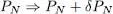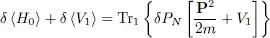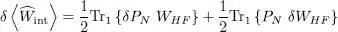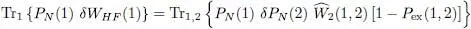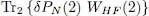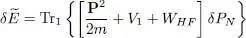This operator is Hermitian, since, as the two operators P exand W 2are Hermitian and commute, we can write:
(59) 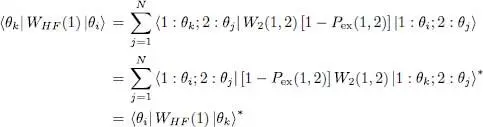
Furthermore, we recognize in (58)the matrix element of a partial trace on particle 2 (Complement E III, § 5-b):
(60) 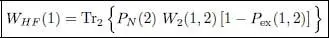
where the projector PN has been introduced inside the trace to limit the sum over j to its first N terms, as in (57). The one-particle operator WHF (1) is thus the partial trace over a second particle (with the arbitrary label 2) of a product of operators acting on both particles. As the summation over j is now taken into account, we are left in (57)with a summation over i , which introduces a trace over the remaining particle 1, and we get:
(61) 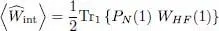
This average value depends on the subspace chosen with the variational ket 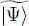 in two ways: explicitly as above, via the projector PN (1) that shows up in the average value (61), but also implicitly via the definition of the Hartree-Fock potential in (60).
in two ways: explicitly as above, via the projector PN (1) that shows up in the average value (61), but also implicitly via the definition of the Hartree-Fock potential in (60).
ϒ. Role of the one-particle reduced density operator
All the average values can be expressed in terms of the projector PN onto the subspace 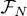 of the space the individual states spanned by the N individual states | θ 1〉, | θ 2〉, ….| θN 〉, which means, according to (50), in terms of the one-particle reduced density operator
of the space the individual states spanned by the N individual states | θ 1〉, | θ 2〉, ….| θN 〉, which means, according to (50), in terms of the one-particle reduced density operator 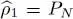 . Hence it is this operator that is the pertinent variable to optimize rather than the set of individual states: certain variations of those states do not change PN , and are meaningless for our purpose.
. Hence it is this operator that is the pertinent variable to optimize rather than the set of individual states: certain variations of those states do not change PN , and are meaningless for our purpose.
Furthermore, the choice of the trial ket 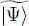 is equivalent to that of PN . In other words, the variational ket
is equivalent to that of PN . In other words, the variational ket 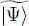 built in (1)does not depend on the basis chosen in the subspace
built in (1)does not depend on the basis chosen in the subspace 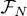 : if we choose in this subspace any orthonormal basis {| uj 〉} other than the {| θj 〉} basis, and if we replace in (1)the
: if we choose in this subspace any orthonormal basis {| uj 〉} other than the {| θj 〉} basis, and if we replace in (1)the 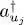 by the
by the  , the ket will remain the same (to within a non-relevant phase factor) as we now show. As seen in § A-6 of Chapter XV, each operator
, the ket will remain the same (to within a non-relevant phase factor) as we now show. As seen in § A-6 of Chapter XV, each operator 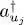 is a linear combination of the
is a linear combination of the  , so that in the product of all the
, so that in the product of all the 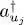 ( j = 1, 2, .. N ) we will find products of N operators
( j = 1, 2, .. N ) we will find products of N operators  . Relation (A-43) of Chapter XVhowever indicates that the squares of any creation operators are zero, which means that the only non-zero products are those including once and only once each of the N different operators
. Relation (A-43) of Chapter XVhowever indicates that the squares of any creation operators are zero, which means that the only non-zero products are those including once and only once each of the N different operators  . Each term is then proportional to the ket
. Each term is then proportional to the ket 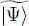 built from the
built from the  . Consequently, the two variational kets built from the two bases are necessarily proportional. As definition (1)ensures they are also normalized, they can only differ by a phase factor, which means they are equivalent from a physical point of view. It is thus the operator
. Consequently, the two variational kets built from the two bases are necessarily proportional. As definition (1)ensures they are also normalized, they can only differ by a phase factor, which means they are equivalent from a physical point of view. It is thus the operator 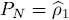 that best embodies the trial ket
that best embodies the trial ket 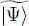 .
.
2-b. Optimization of the one-particle density operator
We now vary 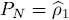 to look for the stationary conditions for the total energy:
to look for the stationary conditions for the total energy:
(62) 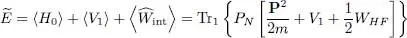
We therefore consider the variation:
(63) 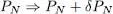
which leads to the following variations for the average values of the one-particle operators:
(64) 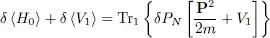
As for the interaction energy, we get two terms:
(65) 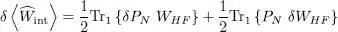
which are actually equal since:
(66) 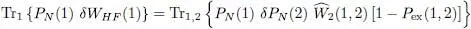
and we recognize in the right-hand side of this expression the trace:
(67) 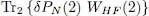
As we can change the label of the particle from 2 to 1 without changing the trace, the two terms of the interaction energy are equal. As a result, we end up with the energy variation:
(68) 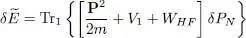
Читать дальше

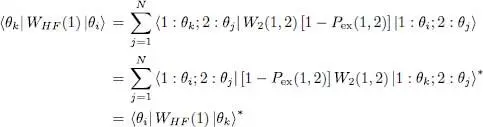
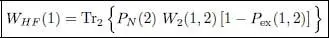
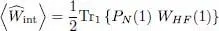
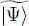 in two ways: explicitly as above, via the projector PN (1) that shows up in the average value (61), but also implicitly via the definition of the Hartree-Fock potential in (60).
in two ways: explicitly as above, via the projector PN (1) that shows up in the average value (61), but also implicitly via the definition of the Hartree-Fock potential in (60).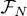 of the space the individual states spanned by the N individual states | θ 1〉, | θ 2〉, ….| θN 〉, which means, according to (50), in terms of the one-particle reduced density operator
of the space the individual states spanned by the N individual states | θ 1〉, | θ 2〉, ….| θN 〉, which means, according to (50), in terms of the one-particle reduced density operator 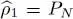 . Hence it is this operator that is the pertinent variable to optimize rather than the set of individual states: certain variations of those states do not change PN , and are meaningless for our purpose.
. Hence it is this operator that is the pertinent variable to optimize rather than the set of individual states: certain variations of those states do not change PN , and are meaningless for our purpose.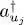 by the
by the  , the ket will remain the same (to within a non-relevant phase factor) as we now show. As seen in § A-6 of Chapter XV, each operator
, the ket will remain the same (to within a non-relevant phase factor) as we now show. As seen in § A-6 of Chapter XV, each operator 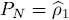 that best embodies the trial ket
that best embodies the trial ket