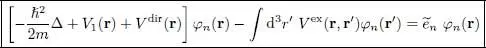1-d. Equivalent formulation for the average energy stationarity
Operator 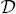 can be diagonalized in the subspace
can be diagonalized in the subspace 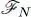 , as can be shown 3 from its definition (36)– a more direct demonstration will be given in § 2. We call φn ( r) its eigenfunctions. These functions φn ( r) are linear combinations of the θj ( r) corresponding to the states appearing in the trial ket (1), and therefore lead to the same N -particle state, because of the antisymmetrization 4 . The basis change from the θi ( r) to the φn ( r) has no effect on the projector PN onto to the subspace
, as can be shown 3 from its definition (36)– a more direct demonstration will be given in § 2. We call φn ( r) its eigenfunctions. These functions φn ( r) are linear combinations of the θj ( r) corresponding to the states appearing in the trial ket (1), and therefore lead to the same N -particle state, because of the antisymmetrization 4 . The basis change from the θi ( r) to the φn ( r) has no effect on the projector PN onto to the subspace 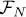 , whose matrix elements appearing in (36)can be expressed in a way similar to those in (20):
, whose matrix elements appearing in (36)can be expressed in a way similar to those in (20):
(37) 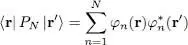
Consequently, the eigenfunctions of the operator 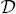 obey the equations:
obey the equations:
(38) 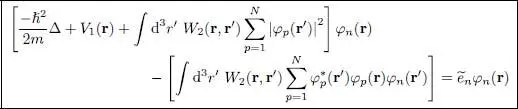
where 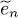 are the associated eigenvalues. These relations are called the “Hartree-Fock equations”.
are the associated eigenvalues. These relations are called the “Hartree-Fock equations”.
For the average total energy associated with a state such as (1)to be stationary, it is therefore necessary for this state to be built from N individual states whose orthogonal wave functions φ 1, φ 2, .. , φN are solutions of the Hartree-Fock equations (38)with n = 1, 2, .. , N . Conversely, this condition is sufficient since, replacing the θj ( r) by solutions φn ( r) of the Hartree-Fock equations in the energy variation (34)yields the result:
(39) 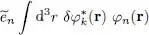
which is zero for all δφk ( r) variations, since, according to (32), they must be orthogonal to the N solutions φn ( r). Conditions (38)are thus equivalent to energy stationarity.
Assume we found a series of solutions for the Hartree-Fock equations, i.e. a set of N eigenfunctions φn ( r) with the associated eigenvalues 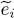 . We still have to compute the minimal variational energy of the N -particle system. This energy is given by the sum (26)of the three terms of kinetic, potential and interaction energies obtained by replacing in (15), (16)and (18)the θi ( r) by the eigenfunctions φn ( r):
. We still have to compute the minimal variational energy of the N -particle system. This energy is given by the sum (26)of the three terms of kinetic, potential and interaction energies obtained by replacing in (15), (16)and (18)the θi ( r) by the eigenfunctions φn ( r):
(40) 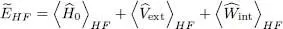
(the subscripts HF indicate we are dealing with the average energies after the Hartree-Fock optimization, which minimizes the variational energy). Intuitively, one could expect this total energy to be simply the sum of the energies 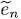 , but, as we are going to show, this is not the case. Multiplying the left-hand side of equation (38)by
, but, as we are going to show, this is not the case. Multiplying the left-hand side of equation (38)by 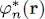 and after integration over d 3 r , we get:
and after integration over d 3 r , we get:
(41) 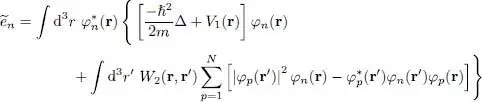
We then take a summation over the subscript n , and use (15), (16)and (18), the θ being replaced by the φ :
(42) 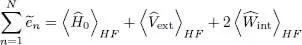
This expression does not yield the stationary value of the total energy, but rather a sum where the particle interaction energy is counted twice. From a physical point of view, it is clear that if each particle energy is computed taking into account its interaction with all the others, and if we then add all these energies, we get an expression that includes twice the interaction energy associated with each pair of particles.
The sum of the 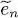 does contain, however, useful information that enables us to avoid computing the interaction energy contribution to the variational energy. Eliminating
does contain, however, useful information that enables us to avoid computing the interaction energy contribution to the variational energy. Eliminating 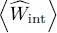 between (40)and (42), we get:
between (40)and (42), we get:
(43) 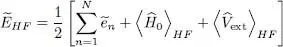
where the interaction energy is no longer present. One can then compute 〈 Ĥ 0〉 HFand 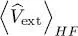 using the solutions of the Hartree-Fock equations (38), without worrying about the interaction energy. Using (15)and (17)in this relation, we can write the total energy
using the solutions of the Hartree-Fock equations (38), without worrying about the interaction energy. Using (15)and (17)in this relation, we can write the total energy 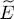 as:
as:
(44) 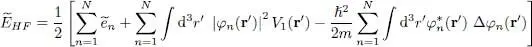
The total energy is thus half the sum of the 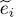 , of the average kinetic energy, and finally of the one-body average potential energy.
, of the average kinetic energy, and finally of the one-body average potential energy.
1-f. Hartree-Fock equations
Equation (38)may be written as:
(45) 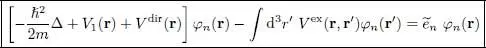
Читать дальше

 can be diagonalized in the subspace
can be diagonalized in the subspace 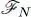 , as can be shown 3 from its definition (36)– a more direct demonstration will be given in § 2. We call φn ( r) its eigenfunctions. These functions φn ( r) are linear combinations of the θj ( r) corresponding to the states appearing in the trial ket (1), and therefore lead to the same N -particle state, because of the antisymmetrization 4 . The basis change from the θi ( r) to the φn ( r) has no effect on the projector PN onto to the subspace
, as can be shown 3 from its definition (36)– a more direct demonstration will be given in § 2. We call φn ( r) its eigenfunctions. These functions φn ( r) are linear combinations of the θj ( r) corresponding to the states appearing in the trial ket (1), and therefore lead to the same N -particle state, because of the antisymmetrization 4 . The basis change from the θi ( r) to the φn ( r) has no effect on the projector PN onto to the subspace 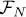 , whose matrix elements appearing in (36)can be expressed in a way similar to those in (20):
, whose matrix elements appearing in (36)can be expressed in a way similar to those in (20):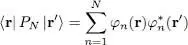
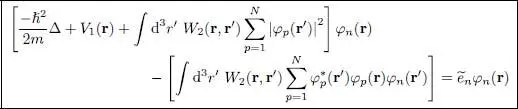
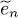 are the associated eigenvalues. These relations are called the “Hartree-Fock equations”.
are the associated eigenvalues. These relations are called the “Hartree-Fock equations”.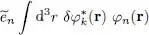
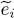 . We still have to compute the minimal variational energy of the N -particle system. This energy is given by the sum (26)of the three terms of kinetic, potential and interaction energies obtained by replacing in (15), (16)and (18)the θi ( r) by the eigenfunctions φn ( r):
. We still have to compute the minimal variational energy of the N -particle system. This energy is given by the sum (26)of the three terms of kinetic, potential and interaction energies obtained by replacing in (15), (16)and (18)the θi ( r) by the eigenfunctions φn ( r):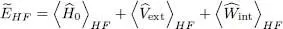
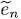 , but, as we are going to show, this is not the case. Multiplying the left-hand side of equation (38)by
, but, as we are going to show, this is not the case. Multiplying the left-hand side of equation (38)by 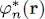 and after integration over d 3 r , we get:
and after integration over d 3 r , we get: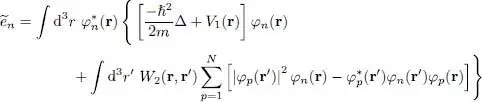
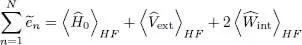
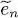 does contain, however, useful information that enables us to avoid computing the interaction energy contribution to the variational energy. Eliminating
does contain, however, useful information that enables us to avoid computing the interaction energy contribution to the variational energy. Eliminating 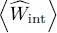 between (40)and (42), we get:
between (40)and (42), we get: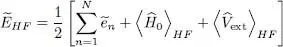
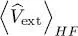 using the solutions of the Hartree-Fock equations (38), without worrying about the interaction energy. Using (15)and (17)in this relation, we can write the total energy
using the solutions of the Hartree-Fock equations (38), without worrying about the interaction energy. Using (15)and (17)in this relation, we can write the total energy 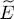 as:
as: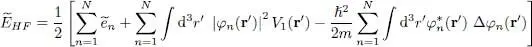
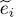 , of the average kinetic energy, and finally of the one-body average potential energy.
, of the average kinetic energy, and finally of the one-body average potential energy.