We now vary 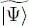 to determine the conditions leading to a stationary value of the total energy
to determine the conditions leading to a stationary value of the total energy 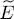 :
:
(26) 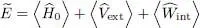
where the three terms in this summation are given by (15), (16)and (18). Let us vary one of the kets | θk 〉, k being arbitrarily chosen between 1 and N :
(27) 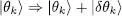
or, in terms of an individual wave function:
(28) 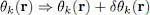
This will yield the following variations:
(29) 
and:
(30) 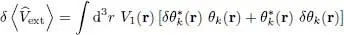
As for the variation of  , we must take from (18)two contributions: the first one from the terms i = k , and the other from the terms j = k . These contributions are actually equal as they only differ by the choice of a dummy subscript. The factor 1/2 disappears and we get:
, we must take from (18)two contributions: the first one from the terms i = k , and the other from the terms j = k . These contributions are actually equal as they only differ by the choice of a dummy subscript. The factor 1/2 disappears and we get:
(31) 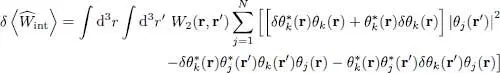
The variation of 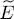 is simply the sum of (29), (30)and (31).
is simply the sum of (29), (30)and (31).
We now consider variations δθk , which can be written as:
(32) 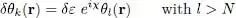
(where δε is a first order infinitely small parameter). These variations are proportional to the wave function of one of the non-occupied states, which was added to the occupied states to form a complete orthonormal basis; the phase χ is an arbitrary parameter. Such a variation does not change, to first order, either the norm of | θk 〉, or its scalar product with all the occupied states l ≤ N ; it therefore leaves unchanged our assumption that the occupied states basis is orthonormal. The first order variation of the energy 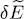 is obtained by inserting δθk and its complex conjugate
is obtained by inserting δθk and its complex conjugate 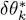 into (29), (30)and (31); we then get terms in eiχ in the first case, and terms in e–iχ in the second. For
into (29), (30)and (31); we then get terms in eiχ in the first case, and terms in e–iχ in the second. For 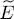 to be stationary, its variation must be zero to first order for any value of χ ; now the sum of a term in eiχ and another in eiχ will be zero for any value of χ only if both terms are zero. It follows that we can impose
to be stationary, its variation must be zero to first order for any value of χ ; now the sum of a term in eiχ and another in eiχ will be zero for any value of χ only if both terms are zero. It follows that we can impose 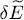 to be zero (stationary condition) considering the variations of δθk and
to be zero (stationary condition) considering the variations of δθk and 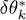 to be independent. Keeping only the terms in
to be independent. Keeping only the terms in 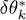 , we obtain the stationary condition of the variational energy:
, we obtain the stationary condition of the variational energy:
(33) 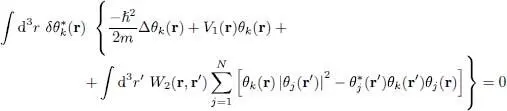
or, taking (20)into account:
(34) 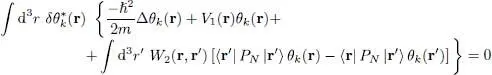
This relation can also be written as::
(35) 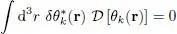
where the integro-differential operator 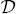 is defined by its action on an arbitrary function θ ( r):
is defined by its action on an arbitrary function θ ( r):
(36) 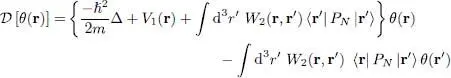
This operator depends on the diagonal 〈 r′| PN | r′〉 and non-diagonal 〈 r′| PN | r′〉 spatial correlation functions associated with the set of states occupied by the N fermions.
Relation (35)thus shows that the action of the differential operator 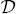 on the function θk ( r) yields a function orthogonal to all the functions θl ( r) for l > N . This means that the function
on the function θk ( r) yields a function orthogonal to all the functions θl ( r) for l > N . This means that the function 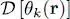 only has components on the wave functions of the occupied states: it is a linear combination of these functions. Consequently, for the energy
only has components on the wave functions of the occupied states: it is a linear combination of these functions. Consequently, for the energy 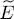 to be stationary there is a simple condition: the invariance under the action of the integro-differential operator
to be stationary there is a simple condition: the invariance under the action of the integro-differential operator 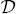 of the N -dimensional vector space
of the N -dimensional vector space 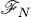 , spanned by all the linear combinations of the functions θi ( r) with i = 1, 2, .. N .
, spanned by all the linear combinations of the functions θi ( r) with i = 1, 2, .. N .
Comment:
One could wonder why we limited ourselves to the variations δθk written in (32), proportional to non-occupied individual states. The reason will become clearer in § 2, where we use a more general method that shows directly which variations of each individual states are really useful to consider (see in particular the discussion at the end of § 2-a). For now, it can be noted that choosing a variation δθk proportional to the same wave function θk ( r) would simply change its norm or phase, and therefore have no impact on the associated quantum state (in addition, a change of norm would not be compatible with our hypotheses, as in the computation of the average values we always assumed the individual states to remain normalized). If the state does not change, the energy 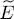 must remain constant and writing a stationary condition is pointless. Similarly, to give θk ( r) a variation proportional to another occupied wave function θl ( r) (where l is included between 1 and N ) is just as useless, as we now show. In this operation, the creation operator
must remain constant and writing a stationary condition is pointless. Similarly, to give θk ( r) a variation proportional to another occupied wave function θl ( r) (where l is included between 1 and N ) is just as useless, as we now show. In this operation, the creation operator 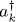 acquires a component on
acquires a component on 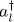 ( Chapter XV, § A-6), but the state vector expression (1)remains unchanged. The state vector thus acquire a component including the square of a creation operator, which is zero for fermions. Consequently, the stationarity of the energy is automatically ensured in this case.
( Chapter XV, § A-6), but the state vector expression (1)remains unchanged. The state vector thus acquire a component including the square of a creation operator, which is zero for fermions. Consequently, the stationarity of the energy is automatically ensured in this case.
Читать дальше

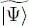 to determine the conditions leading to a stationary value of the total energy
to determine the conditions leading to a stationary value of the total energy 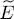 :
: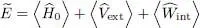
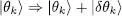
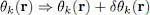

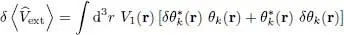
 , we must take from (18)two contributions: the first one from the terms i = k , and the other from the terms j = k . These contributions are actually equal as they only differ by the choice of a dummy subscript. The factor 1/2 disappears and we get:
, we must take from (18)two contributions: the first one from the terms i = k , and the other from the terms j = k . These contributions are actually equal as they only differ by the choice of a dummy subscript. The factor 1/2 disappears and we get: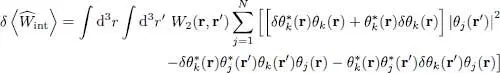
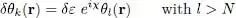
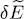 is obtained by inserting δθk and its complex conjugate
is obtained by inserting δθk and its complex conjugate 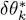 into (29), (30)and (31); we then get terms in eiχ in the first case, and terms in e–iχ in the second. For
into (29), (30)and (31); we then get terms in eiχ in the first case, and terms in e–iχ in the second. For 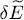 to be zero (stationary condition) considering the variations of δθk and
to be zero (stationary condition) considering the variations of δθk and 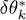 to be independent. Keeping only the terms in
to be independent. Keeping only the terms in 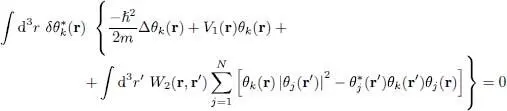
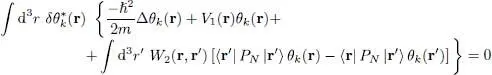
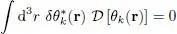
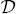 is defined by its action on an arbitrary function θ ( r):
is defined by its action on an arbitrary function θ ( r):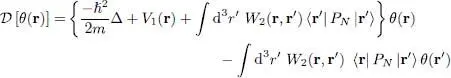
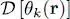 only has components on the wave functions of the occupied states: it is a linear combination of these functions. Consequently, for the energy
only has components on the wave functions of the occupied states: it is a linear combination of these functions. Consequently, for the energy 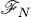 , spanned by all the linear combinations of the functions θi ( r) with i = 1, 2, .. N .
, spanned by all the linear combinations of the functions θi ( r) with i = 1, 2, .. N .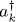 acquires a component on
acquires a component on 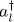 ( Chapter XV, § A-6), but the state vector expression (1)remains unchanged. The state vector thus acquire a component including the square of a creation operator, which is zero for fermions. Consequently, the stationarity of the energy is automatically ensured in this case.
( Chapter XV, § A-6), but the state vector expression (1)remains unchanged. The state vector thus acquire a component including the square of a creation operator, which is zero for fermions. Consequently, the stationarity of the energy is automatically ensured in this case.










