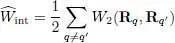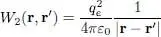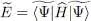However, be it in atoms or in solids, the repulsion between electrons plays an essential role. Neglecting it would lead us to conclude, for example, that, as Z increases, the size of atoms decreases due to the attractive effect of the nucleus, whereas the opposite occurs 2 ! For N interacting particles, even without taking the spin into account, an exact computation would require solving a Schrödinger equation in a 3 N -dimensional space; this is clearly impossible when N becomes large, even with the most powerful computer. Hence, approximation methods are needed, and the most common one is the Hartree-Fock method, which reduces the problem to solving a series of 3-dimensional equations. It will be explained in this complement for fermionic particles.
The Hartree-Fock method is based on the variational approximation (Complement E XI), where we choose a trial family of state vectors, and look for the one that minimizes the average energy. The chosen family is the set of all possible Fock states describing the system of N fermions. We will introduce and compute the “self-consistent” mean field in which each electron moves; this mean field takes into account the repulsion due to the other electrons, hence justifying the central field method discussed in Complement A XIV. This method applies not only to the atom’s ground state but also to all its stationary states. It can also be generalized to many other systems such as molecules, for example, or to the study of the ground level and excited states of nuclei, which are protons and neutrons in bound systems.
This complement presents the Hartree-Fock method in two steps, starting in § 1 with a simple approach in terms of wave functions, which is then generalized in § 2 by using Dirac notation and projector operators. The reader may choose to go through both steps or go directly to the second. In § 1, we deal with spinless particles, which allows discussing the basic physical ideas and introducing the mean field concept keeping the formalism simple. A more general point of view is exposed in § 2, to clarify a number of points and to introduce the concept of a one-particle (with or without spin) effective Hartree-Fock Hamiltonian. This Hamiltonian reduces the interactions with all the other particles to a mean field operator. More details on the Hartree-Fock methods, and in particular their relations with the Wick theorem, can be found in Chapters 7 and 8 of reference [5].
1. Foundation of the method
Let us first expose the foundation of the Hartree-Fock method in a simple case where the particles have no spin (or are all in the same individual spin state) so that no spin quantum number is needed to define their individual states, specified by their wave functions. We introduce the notation and define the trial family of the N -particle state vectors.
1-a. Trial family and Hamiltonian
We choose as the trial family for the state of the N -fermion system all the states that can be written as:
(1) 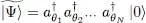
where 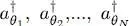 are the creation operators associated with a set of normalized individual states | θ 1〉, | θ 2〉, | θ N〉, all orthogonal to each other (and hence distinct). The state
are the creation operators associated with a set of normalized individual states | θ 1〉, | θ 2〉, | θ N〉, all orthogonal to each other (and hence distinct). The state 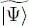 is therefore normalized to 1. This set of individual states is, at the moment, arbitrary; it will be determined by the following variational calculation.
is therefore normalized to 1. This set of individual states is, at the moment, arbitrary; it will be determined by the following variational calculation.
For spinless particles, the corresponding wave function 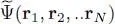 can be written in the form of a Slater determinant (Chapter XIV, § C-3- c - β ):
can be written in the form of a Slater determinant (Chapter XIV, § C-3- c - β ):
(2) 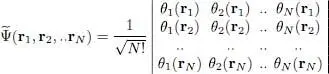
The system Hamiltonian is the sum of the kinetic energy, the one-body potential energy and the interaction energy:
(3) 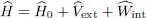
The first term, Ĥ 0, is the operator associated with the fermion kinetic energy, sum of the individual kinetic energies:
(4) 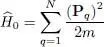
where m is the particle mass and P q, the momentum operator of particle q . The second term, 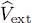 , is the operator associated with their energy in an applied external potential V 1:
, is the operator associated with their energy in an applied external potential V 1:
(5) 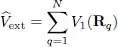
where R qis the position operator of particle q . For electrons with charge qe placed in the attractive Coulomb potential of a nucleus of charge — Zqe positioned at the origin ( Z is the nucleus atomic number), this potential is attractive and equal to:
(6) 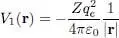
where ε 0is the vacuum permittivity. Finally, the term 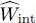 corresponds to their mutual interaction energy:
corresponds to their mutual interaction energy:
(7) 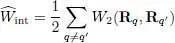
For electrons, the function W 2is given by the Coulomb repulsive interaction:
(8) 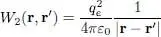
The expressions given above are just examples; as mentioned earlier, the Hartree-Fock method is not limited to the computation of the electronic energy levels in an atom.
1-b. Energy average value
Since state (1)is normalized, the average energy in this state is given by:
(9) 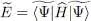
Let us evaluate successively the contributions of the three terms of (3), to obtain an expression which we will eventually vary.
Let us introduce a complete orthonormal basis {| θs } of the one-particle state space by adding to the set of states | θi ( i = 1, 2, N ) other orthonormal states; the subscript s now ranges from 1 to D , dimension of this space ( D may be infinite). We can then expand Ĥ 0as in relation (B-12) of Chapter XV:
Читать дальше

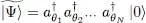
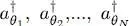 are the creation operators associated with a set of normalized individual states | θ 1〉, | θ 2〉, | θ N〉, all orthogonal to each other (and hence distinct). The state
are the creation operators associated with a set of normalized individual states | θ 1〉, | θ 2〉, | θ N〉, all orthogonal to each other (and hence distinct). The state 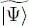 is therefore normalized to 1. This set of individual states is, at the moment, arbitrary; it will be determined by the following variational calculation.
is therefore normalized to 1. This set of individual states is, at the moment, arbitrary; it will be determined by the following variational calculation.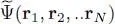 can be written in the form of a Slater determinant (Chapter XIV, § C-3- c - β ):
can be written in the form of a Slater determinant (Chapter XIV, § C-3- c - β ):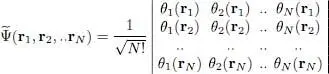
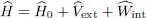
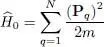
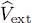 , is the operator associated with their energy in an applied external potential V 1:
, is the operator associated with their energy in an applied external potential V 1: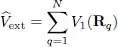
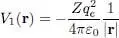
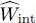 corresponds to their mutual interaction energy:
corresponds to their mutual interaction energy: