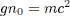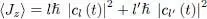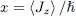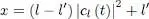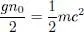Claude Cohen-Tannoudji - Quantum Mechanics, Volume 3

As for the interaction term (term in g on the left-hand side), we can express it in a more convenient way, defining as before the numerical density n 0:

(75)

and using the definition (39)for the sound velocity c . It can then be written in a form similar to (74):

(76)

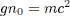
The two velocities vl and c allow an easy comparison of the respective importance of the kinetic and potential energies in a state l .

We now compare the contributions of these two terms either for states with a given l , or for a superposition of states (63). To clarify the discussion and be able to draw a figure, we will use a continuous variable defined as the average 〈 Jz 〉 of the component along Oz of the angular momentum:

(77)

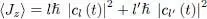
This expression varies continuously between lħ and l′ħ when the relative weights of | cl ( t )| 2and | cl' ( t )| 2are changed while imposing relation (64); the continuous variable:

(78)

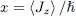
allows making interpolations between the discrete integer values of l .

Using the normalization relation (64)of the wave function (63), we can express x as a function of | cl′ ( t )| 2:

(79)

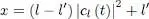
The variable x characterizes the modulus of each of the two components of the variational function (63). A second variable is needed to define the relative phase between these two components, which comes into play for example in (66). Instead of studying the time evolution of the fluid state vector inside this variational family, we shall simply give a qualitative argument, for several reasons. First of all, it is not easy to characterize precisely the coupling between the fluid and the environment by a Hamiltonian that can change the fluid rotational angular momentum (for example, the wall’s irregularities may transfer energy and angular momentum from the fluid to the container). Furthermore, as the time-dependent Gross-Pitaevskii equation is nonlinear, its precise solutions are generally found numerically. This is why we shall only qualitatively discuss the effects of the potential barrier found in §3-b. The higher this barrier, the more difficult it is for x to go from l to l ’. Let us evaluate the variation of the average energy as a function of x .

For integer values of x , relation (74)shows that the average rotational kinetic energy varies as the square of x ; in between, its value can be found by interpolation as in (77). As for the potential energy, we saw that a continuous variation of cl ( t ) and cl′ ( t ) necessarily involves a coherent superposition, which has an energy cost and increases the repulsive potential interaction. In particular, this interaction energy is multiplied by the factor 3/2 when the moduli of cl ( t ) and cl′ ( t ) are equal (i.e. when x is an integer plus 1/2). As a result, to the quadratic variation of the rotational kinetic energy, we must add an oscillating variation of the potential energy, minimum for all the integer values of x , and maximum half-way between. The oscillation amplitude is given by:

(80)

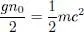
Figure 3shows three plots of the variation of the system energy as a function of the average value 〈 Jz 〉. The lowest one, shown as a dotted line, corresponds to a superposition of the state l with the state l ’ = l — 1, for a very small value of the coupling constant g (weak interactions, gas almost ideal). In this case and according to (39), the sound velocity is also very small and we are in the case c ≪ vl . Comparing (74)and (80)then shows that the potential energy contribution is negligible compared to the variation of the rotational kinetic energy between the two states. As a result, the modulation on this dotted line is barely perceptible, and this curve presents a single minimum at x = 0: whatever the initial rotational state, no potential barrier prevents the fluid rotational velocity from returning to zero (for example under the effect of the interactions with the irregularities of the walls containing the fluid).

The other two curves in Figure 3correspond to a much larger value of g , hence, according to (39), to a much higher value of c . There are now several values of l for which vl is small compared to c . The dashed line corresponds, as for the previous curve, to a superposition of the two states l = 1 and l ′ = l — 1; the solid line (for the same value of g ) to a superposition of l = 3 and l ′ = 0, corresponding to the case where the system goes directly from the state l = 3 to the rotational ground state in the torus, with l ′ = 0. It is obviously this last curve that presents the lowest energy barrier starting from l = 3 (shown with a circle in the figure). This is normal since this is the curve that involves the largest variation in the kinetic energy, in a sense opposite to that of the potential energy variation. It is thus the direct transition from l = 3 to l′ = 0 that will determine the possibility for the system to relax towards a state of slower rotation. Let us again use (74)and (80)to compare the kinetic energy variation and the height of the repulsive potential barrier. All the states l , with velocities vl much larger than c , have a kinetic energy much bigger than the maximum value of the potential energy: no energy barrier can be formed. On the other hand, all the states l with velocities vl much smaller than c cannot lower their rotational state without going over a potential barrier.

In between these two extreme cases, there exists (for a given g ) a “critical” value lc corresponding to the onset of the barrier. It is associated with a “critical velocity” vc = lcħ / mr , of the order of the sound velocity c , fixing the maximum value of vl for which this potential barrier exists. If the fluid rotational velocity in the torus is greater than vc , the liquid can slow down its rotation without going over an energy barrier, and dissipation occurs as in an ordinary viscous liquid – the fluid is said to be “normal”. If, however, the fluid velocity is less than the critical velocity, the physical system must necessarily go over a potential barrier (or more) to continuously tend towards l = 0. As this barrier results from the repulsion between all the particles and their neighbors, it has a macroscopic value. In principle, any barrier can be overcome, be it by thermal excitation, or by the quantum tunnel effect. However the time needed for this passage may take a gigantic value. First of all, it is extremely unlikely for a thermal fluctuation to reach a macroscopic energy value. As for the tunnel effect, its transition probability decreases exponentially with the barrier height and becomes extremely low for a macroscopic object. Consequently, the relaxation times of the fluid velocity may become extraordinarily large, and, on the human scale, the rotation can be considered to last indefinitely. This phenomenon is called “superfluidity”.