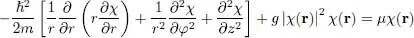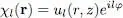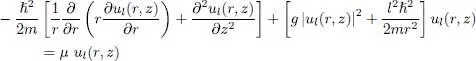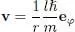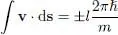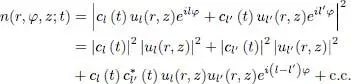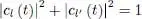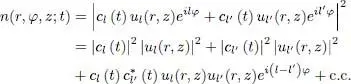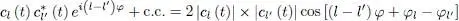3-a. Toroidal geometry, quantization of the circulation, vortex
To prevent any confusion with the azimuthal angle φ we now call χ the Gross-Pitaevskii wave function. The time-independent Gross-Pitaevskii equation then becomes (in the absence of any potential except the wall potentials of the box):
(58) 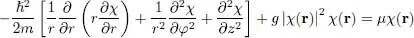
We look for solutions of the form:
(59) 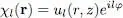
where l is necessarily an integer (otherwise the wave function would be multi-valued). Such a solution has an angular momentum with a well defined component along Oz , equal to lħ per atom. Inserting this expression in (58), we obtain the equation for ul ( r , z ):
(60) 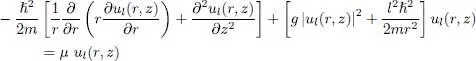
which must be solved with the boundary conditions imposed by the torus shape to obtain the ground state (associated with the lowest value of μ ). The term in l 2 ħ 2/2 mr 2is simply the rotational kinetic energy around Oz . If the tore radius R is very large compared to the size of its cross-section, the term l 2/ r 2may, to a good approximation, be replaced by the constant l 2/ R 2. It follows that the same solution of (60)is valid for any value of l as long as the chemical potential is increased accordingly. Each value of the angular momentum thus yields a ground state and the larger l , the higher the corresponding chemical potential. All the coefficients of the equation being real, we shall assume, from now on, the functions ul ( r , z ) to be real.
As the wave function is of the form (59), its phase only depends on φ and expression (51)for the fluid velocity is written as:
(61) 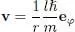
where e φis the tangential unit vector (perpendicular both to rand the Oz axis). Consequently, the fluid rotates along the toroidal tube, with a velocity proportional to l . As vis a gradient, its circulation along a closed loop “equivalent to zero” (i.e. which can be contracted continuously to a point) is zero. If the closed loop goes around the tore, the path is no longer equivalent to zero and its circulation may be computed along a circle where r and z remain constant, and φ varies from 0 to 2π; as the path length equals 2π r , we get:
(62) 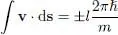
(with a + sign if the rotation is counterclockwise and a — sign in the opposite case). As l is an integer, the velocity circulation around the center of the tore is quantized in units of h/m . This is obviously a pure quantum property (for a classical fluid, this circulation can take on a continuous set of values).
To simplify the calculations, we have assumed until now that the fluid rotates as a whole inside the toroidal ring. More complex fluid motions, with different geometries, are obviously possible. An important case, which we will return to later, concerns the rotation around an axis still parallel to Oz , but located inside the fluid. The Gross-Pitaevskii wave function must then be zero along a line inside the fluid itself, which thus contains a singular line. This means that the phase may change by 2π as one rotates around this line. This situation corresponds to what is called a “vortex”, a little swirl of fluid rotating around the singular line, called the “vortex core line”. As the circulation of the velocity only depends on the phase change along the path going around the vortex core, the quantization relation (62)remains valid. Actually, from a historical point of view, the Gross-Pitaevskii equation was first introduced for the study of superfluidity and the quantization of the vortices circulation.
3-b. Repulsive potential barrier between states of different l
A classical rotating fluid will always come to rest after a certain time, due to the viscous dissipation at the walls. In such a process, the macroscopic rotational kinetic energy of the whole fluid is progressively degraded into numerous smaller scale excitations, which end up simply heating the fluid. Will a rotating quantum fluid of repulsive bosons, described by a wave function χl ( r), behave in the same way? Will it successively evolve towards the state χ l – 1( r), then χ l -2( r), etc., until it comes to rest in the state χ 0( r)?
We have seen in § 4-c of Complement C XVthat, to avoid the energy cost of fragmentation, the system always remains in a state where all the particles occupy the same quantum state. This is why we can use the Gross-Pitaevskii equation (18).
Let us first assume that the wave function χ( r, t ) changes smoothly from χl ( r) to χ l′( r) according to:
(63) 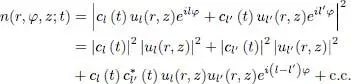
where the modulus of cl ( t ) decreases with time from 1 to 0, whereas cl′ ( t ) does the opposite. Normalization imposes that at all times t :
(64) 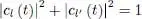
In such a state, let us show that the numerical density n ( r , φ , z ; t ) now depends on φ (this was not the case for either states l or l ′ separately). The transverse dependence of the density as a function of the variables r and z , is barely affected 3 . The variations of n ( r , φ , z ; t ) are given by:
(65) 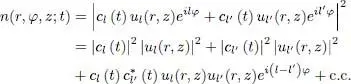
where c.c. stands for the complex conjugate of the preceding factor. The first two terms are independent of φ , and are just a weighted average of the densities associated with each of the states l and l ′. The last term oscillates as a function of φ with an amplitude | cl ( t )| × | cl ′ ( t )|, which is only zero if one of the two coefficients cl ( t ) or cl ′ ( t ) is zero. Calling φl the phase of the coefficient cl ( t ) this last term is proportional to:
(66) 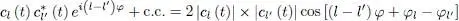
Читать дальше