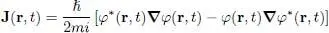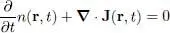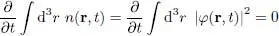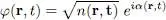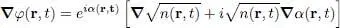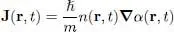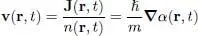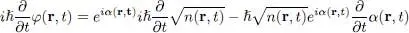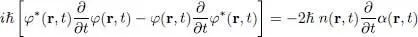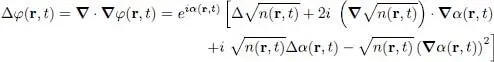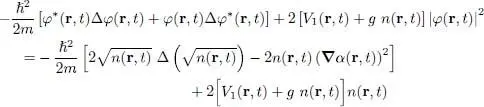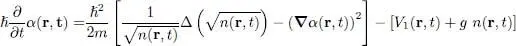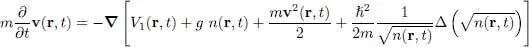Claude Cohen-Tannoudji - Quantum Mechanics, Volume 3

Let us now define a vector J( r, t ) by:

(45)

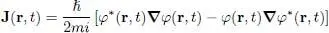
If we compute the divergence of this vector, the terms in ▽ φ * · ▽ φ cancel out and we are left with terms identical to the right-hand side of (44), with the opposite sign. This leads to the conservation equation:

(46)

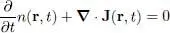
J( r, t) is thus the probability current associated with our boson system. Integrating over all space, using the divergence theorem, and assuming φ ( r, t ) (hence the current) goes to zero at infinity, we obtain:

(47)

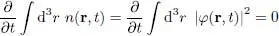
This shows, as announced earlier, that the Gross-Pitaevskii equation conserves the norm of the wave function describing the particle system.

We now set:

(48)

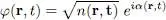
The gradient of this function is written as:

(49)

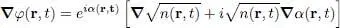
Inserting this result in (45), we get:

(50)

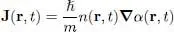
or, defining the particle local velocity v( r, t ) as the ratio of the current to the density:

(51)

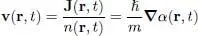
We have defined a velocity field, similar to the velocity field of a fluid in motion in a certain region of space; this field velocity is irrotational (zero curl everywhere).

We now compute the time derivative of this velocity. Taking the derivative of (48), we get:

(52)

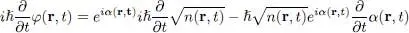
so that we can isolate the time derivative of α ( r, t) by the following combination:

(53)

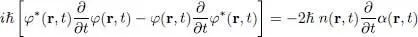
The left-hand side of this relation can be computed with the Gross-Pitaevskii equation (18)and its complex conjugate, as we now show. We first take the divergence of the gradient (49)to obtain the Laplacian:

(54)

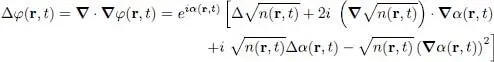
We then insert the time derivative of φ ( r, t ) given by the Gross-Pitaevskii equation (18)in the left-hand side of relation (53), which becomes:

(55)

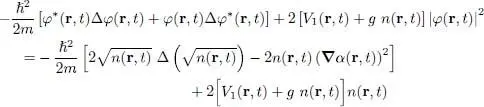
This result must be equal to the right-hand side of (53). We therefore get, after dividing both sides by —2 n ( r, t ):

(56)

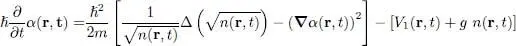
Using (51), we finally obtain the evolution equation for the velocity v( r, t ):

(57)

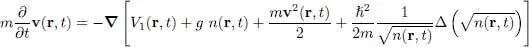
This equation looks like the classical Newton equation. Its right-hand side includes the sum of the forces corresponding to the external potential V 1( r, t ), and to the mean interaction potential with the other particles gn ( r, t ); the third term in the gradient is the classical kinetic energy gradient 1 (as in Bernoulli’s equation of classical hydrodynamics). The only purely quantum term is the last one, as shown by its explicit dependence on ħ 2. It involves spatial derivatives of n ( r, t ), and is only important if the relative variations δn / n of the density occur over small enough distances (for example, this term is zero for a uniform density). This term is sometimes called “quantum potential”, or “quantum pressure term” or, in other contexts, “Bohm potential”. A frequently used approximation is to consider the spatial variations of n ( r, t ) to be slow, which amounts to ignoring this quantum potential term: this is the so-called Thomas-Fermi approximation.

We have found for a system of N particles a series of properties usually associated with the wave function of a single particle, and in particular a local velocity directly proportional to its phase gradient 2 . The only difference is that, for the N -particle case, we must add to the external potential V 1( r, t ) a local interaction potential gn ( r, t ), which does not significantly change the form of the equations but introduces some nonlinearity that can lead to completely new physical effects.

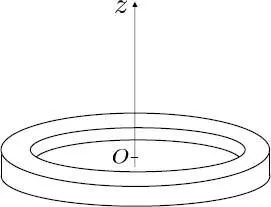
Figure 2: A repulsive boson gas is contained in a toroidal box. All the bosons are supposed to be initially in the same quantum state describing a rotation around the Oz axis. As we explain in the text, this rotation can only slow down if the system overcomes a potential energy barrier that comes from the repulsive interactions between the particles. This prevents any observable damping of the rotation over any accessible time scale; the fluid rotates indefinitely, and is said to be superfluid .

Consider now a system of repulsive bosons contained in a toroidal box with a rotational axis Oz ( Figure 2); the shape of the torus cross-section (circular, rectangular or other) is irrelevant for our argument and we shall use cylindrical coordinates r , φ and z . We first introduce solutions of the Gross-Pitaevskii equation that correspond to the system rotating inside the toroidal box, around the Oz axis. We will then show that these rotational states are metastable, as they can only relax towards lower energy rotational states by overcoming a macroscopic energy barrier: this is the physical origin of superfluidity.