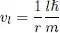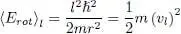Whatever the phases of the two coefficients cl ( t ) and cl′ ( t ), the cosine will always oscillate between — 1 and 1 as a function of φ . Adjusting those phases, one can deliberately change the value of φ for which the density is maximum (or minimum), but this will always occur somewhere on the circle. Superposing two states necessarily modulates the density.
Let us evaluate the consequences of this density modulation on the internal repulsive interaction energy of the fluid. As we did in relation (15), we use for the interaction energy the zero range potential approximation, and insert it in expression (15)of Complement C XV. Taking into account the normalization (17)of the wave function, we get:
(67) 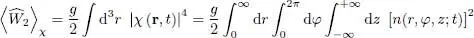
We must now include the square of (65)in this expression, which will yield several terms. The first one, in | cl ( t )| 4, leads to the contribution:
(68) 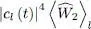
where 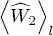 is the interaction energy for the state χ l ( r). The second contribution is the similar term for the state l ′, and the third one, a cross term in 2| cl ( t )| 2| cl′ ( t )| 2. Assuming, to keep things simple, that the densities associated with the states l and l ′ are practically the same, the sum of these three terms is just:
is the interaction energy for the state χ l ( r). The second contribution is the similar term for the state l ′, and the third one, a cross term in 2| cl ( t )| 2| cl′ ( t )| 2. Assuming, to keep things simple, that the densities associated with the states l and l ′ are practically the same, the sum of these three terms is just:
(69) 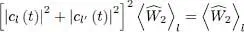
Up to now, the superposition has had no effect on the repulsive internal interaction energy. As for the cross terms between the terms independent of φ in (65)and the terms in e ±i(l – l′)φ, they will cancel out when integrated over φ . We are then left with the cross terms in e ±i(l – l′)φ× e ∓;i(l – l′)φ, whose integral over φ yields:
(70) 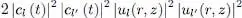
Assuming as before that the densities associated with the states l and l ′ are practically the same, we obtain, after integration over r and z :
(71) 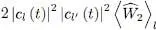
Adding (69), we finally obtain:
(72) 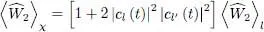
We have shown that the density modulation associated with the superposition of states always increases the internal repulsion energy: this modulation does lower the energy in the low density region, but the increase in the high energy region outweighs the decrease (since the repulsive energy is a quadratic function of the density). The internal energy therefore varies between 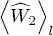 and the maximum (3/2)
and the maximum (3/2) 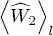 , reached when the moduli of cl ( t ) and cl′ ( t ) are both equal to
, reached when the moduli of cl ( t ) and cl′ ( t ) are both equal to 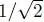 .
.
α. Other geometries, different relaxation channels
There are many other ways for the Gross-Pitaevskii wave function to go from one rotational state to another. We have limited ourselves to the simplest geometry to introduce the concept of energy barriers with minimal mathematics. The fluid could transit, however, through more complex geometries, such as the frequently observed creation of a vortex on the wall, the little swirl we briefly talked about at the end of § 3-a. A vortex introduces a 2π phase shift around a singular line along which the wave function is zero. Once the vortex is created, and contrary to what was the case in (62), the velocity circulation along a loop going around the torus is no longer independent of its path: it will change by 2π ħ / m depending on whether the vortex is included in the loop or not. Furthermore, as the vortex moves in the fluid from one wall to another, it can be shown that the proportion of fluid conserving the initial circulation decreases while the proportion having a circulation where the quantum number l differs by one unit increases. Consequently, this vortex motion changes progressively the rotational angular momentum. Once the vortex has vanished on the other wall, the final result is a decrease by one unit of the quantum number l associated with the fluid rotation.
The continuous passage of vortices from one wall to another therefore yields another mechanism that allows the angular moment of the fluid to decrease. The creation of a vortex, however, is necessarily accompanied by a non-uniform fluid density, described by the Gross-Pitaevskii equation (this density must be zero along the vortex core). As we have seen above, this leads to an increase in the average repulsive energy between the particles (the fluid elastic energy). This process thus also encounters an energy barrier (discussed in more detail in the conclusion). In other words, the creation and motion of vortices provide another “relaxation channel” for the fluid velocity, with its own energy barrier, and associated relaxation time.
Many other geometries can be imagined for changing the fluid flow. Each of them is associated with a potential barrier, and therefore a certain lifetime. The relaxation channel with the shortest lifetime will mainly determine the damping of the fluid velocity, which may take, in certain cases, an extraordinarily long time (dozens of years or more), hence the name of “superfluid”.
3-c. Critical velocity, metastable flow
For the sake of simplicity, we will use in our discussion the simple geometry of § 3-a. The transposition to other geometries involving, for example, the creation of vortices in the fluid would be straightforward. The main change would concern the height of the energy barrier 4 .
With this simple geometry, the potential to be used in (60)is the sum of a repulsive potential g | ul ( r , z )| 2and a kinetic energy of rotation around Oz , equal to l 2 ħ 2/2 mr 2. We now show that, in a given l state, these two contributions can be expressed as a function of two velocities. First, relation (61)yields the rotation velocity vl associated with state l :
(73) 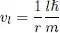
and the rotational energy is simply written as:
(74) 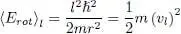
Читать дальше

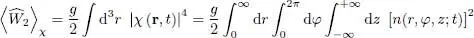
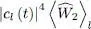
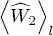 is the interaction energy for the state χ l ( r). The second contribution is the similar term for the state l ′, and the third one, a cross term in 2| cl ( t )| 2| cl′ ( t )| 2. Assuming, to keep things simple, that the densities associated with the states l and l ′ are practically the same, the sum of these three terms is just:
is the interaction energy for the state χ l ( r). The second contribution is the similar term for the state l ′, and the third one, a cross term in 2| cl ( t )| 2| cl′ ( t )| 2. Assuming, to keep things simple, that the densities associated with the states l and l ′ are practically the same, the sum of these three terms is just: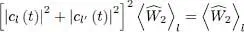
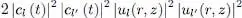
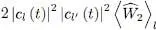
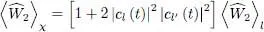
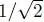 .
.