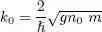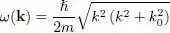(15) 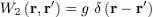
Using definition (13)of the Gross-Pitaevskii potential, we can compute its effect in the position representation, as in Complement C XV. The same calculations as in §§ 2-b- β and 2-b-ϒ of that complement allow showing that relation (12)becomes the Gross-Pitaevskii time-dependent equation ( N is supposed to be large enough to permit replacing N — 1 by N ):
(16) 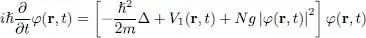
Normalizing the wave function φ ( r, t ) to N :
(17) 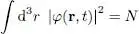
equation (16)simply becomes:
(18) 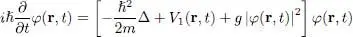
Comment:
It can be shown that this time evolution does conserve the norm of | φ ( t )〉, as required by (3). Without the nonlinear term of (16), it would be obvious since the usual Schrödinger equation conserves the norm. With the nonlinear term present, it will be shown in § 2-a that the norm is still conserved.
1-c. Phonons and Bogolubov spectrum
Still dealing with spinless bosons, we consider a uniform system, at rest, of particles contained in a cubic box of edge length L . The external potential V 1( r) is therefore zero inside the box and infinite outside. This potential may be accounted for by forcing the wave function to be zero at the walls. In many cases, it is however more convenient to use periodic boundary conditions (Complement C XIV, § 1-c), for which the wave function of the individual lowest energy state is simply a constant in the box. We thus consider a system in its ground state, whose Gross-Pitaevskii wave function is independent of r:
(19) 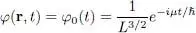
with a μ value that satisfies equation (16):
(20) 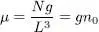
where n 0= N / L 3is the system density. Comparing this expression with relation (58)of Complement C XVallows us to identify μ with the ground state chemical potential. We assume in this section that the interactions between the particles are repulsive (see the comment at the end of the section):
(21) 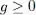
α. Excitation propagation
Let us see which excitations can propagate in this physical system, whose wave function is no longer the function (19), uniform in space. We assume:
(22) 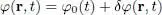
where δφ ( r, t ) is sufficiently small to be treated to first order. Inserting this expression in the right-hand side of (16), and keeping only the first-order terms, we find in the interaction term the first-order expression:
(23) 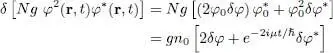
We therefore get, to first-order:
(24) 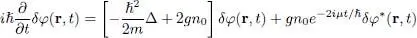
which shows that the evolution of δφ ( r, t ) is coupled to that of δφ *( r, t ). The complex conjugate equation can be written as:
(25) 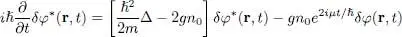
We can make the time-dependent exponentials on the right-hand side disappear by defining:
(26) 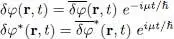
This leads us to a differential equation with constant coefficients, which can be simply expressed in a matrix form:
(27) 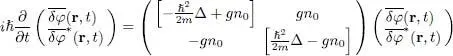
where we have used definition (20)for μ to replace 2 gn 0— μ by gn 0. If we now look for solutions having a plane wave spatial dependence:
(28) 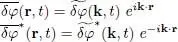
the differential equation can be written as:
(29) 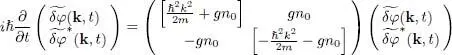
The eigenvalues ħw ( k) of this matrix satisfy the equation:
(30) 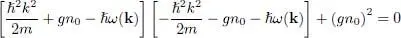
that is:
(31) 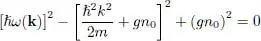
The solution of this equation is:
(32) 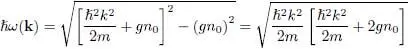
(the opposite value is also a solution, as expected since we calculate at the same time the evolution of 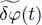 and of its complex conjugate; we only use here the positive value). Setting:
and of its complex conjugate; we only use here the positive value). Setting:
(33) 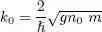
relation (32)can be written:
(34) 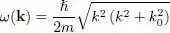
The spectrum given by (32)is plotted in Figure 1, where one sees the intermediate regime between the linear region at low energy, and the quadratic region at higher energy. It is called the “Bogolubov spectrum” of the boson system.
Читать дальше

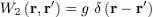
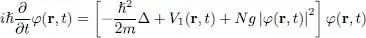
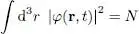
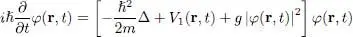
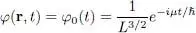
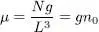
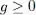
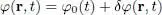
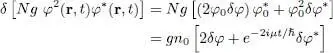
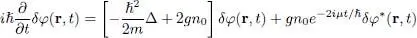
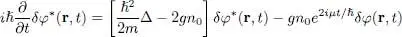
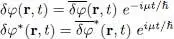
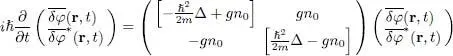
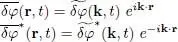
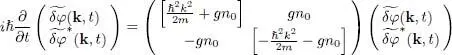
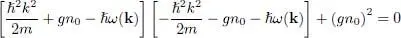
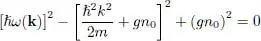
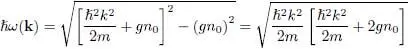
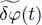 and of its complex conjugate; we only use here the positive value). Setting:
and of its complex conjugate; we only use here the positive value). Setting: