where the direct V dlr( r) and exchange V ex( r, r′) potentials are defined as:
(46) 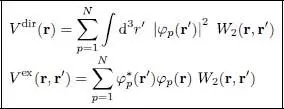
Note that the terms p = n coming from the two potentials cancel each other; hence they can be eliminated from the two summations, without changing the final result. The contribution of the direct potential is sometimes called the “Hartree term”, and the contribution of the exchange potential, the “Fock term”. The first is easy to understand: with the exception of the term p = n , it corresponds to the interaction of a particle at point rwith all the others at points r′, averaged for each of them by its density distribution | φp ( r′)| 2. As for the exchange potential, and in spite of its name, this term is not, strictly speaking, a potential; it is not diagonal in the position representation, even though it basically comes from a particle interaction which is diagonal in that representation. This peculiar non-diagonal form actually comes from the combination of the fermion antisymmetrization and the variational approximation. This exchange potential is homogeneous to a potential divided by the cube of a length. It is obviously a Hermitian operator as it is derived from a potential W 2( r, r′) which is real and symmetric with respect to rand r′.
A more intuitive and simplified version of these equations was suggested by Hartree, in which the exchange potentials are ignored in (45). Without the integral term, these equations become very similar to a series of Schrödinger equations for independent particles, each of them moving in the mean potential created by all the others (still with the exception of the term p = n in the summation). Including the Fock term should, however, lead to more precise calculations.
Using for the potentials their expressions (46), the Hartree-Fock equations (45)become a set of N coupled equations. They are nonlinear, since the direct and exchange potentials depend on the functions φp ( r). Even though they look like linear eigenvalue equations with eigenfunctions φn ( r) as solutions, a linear resolution would actually require knowing in advance the solutions, since these functions also appear in the potentials (46). The term “self-consistent” is used to characterize this type of situation and the solutions φn ( r) it leads to.
There are no general analytical methods to solve nonlinear self-consistent equations of this type, even in their simplified Hartree version, and numerical methods using successive approximations are commonly used. We start from a series of plausible functions 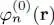 , and compute with (46)the associated potentials. Considering them to be fixed, we obtain linear eigenvalue equations which can be solved quite readily with computers (the single very complicated equation in a 3 N -dimensional space has been replaced by N independent 3-dimensional equations); we have to diagonalize a Hermitian operator to get a new series of orthonormal functions, resulting from the first iteration, and called
, and compute with (46)the associated potentials. Considering them to be fixed, we obtain linear eigenvalue equations which can be solved quite readily with computers (the single very complicated equation in a 3 N -dimensional space has been replaced by N independent 3-dimensional equations); we have to diagonalize a Hermitian operator to get a new series of orthonormal functions, resulting from the first iteration, and called 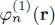 and
and 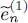 . The second iteration starts from these
. The second iteration starts from these 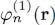 , to compute the new potential values, and get new linear differential equations. Solving these equations yields the next order
, to compute the new potential values, and get new linear differential equations. Solving these equations yields the next order 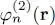 ,
, 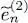 , etc. After a few iterations, one expects the
, etc. After a few iterations, one expects the 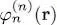 and
and 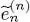 to vary only slightly with the iteration order ( n ), in which case the Hartree-Fock equations have been solved to a good approximation. Using (44)we can then compute the energy we were looking for. It is also possible that physical arguments can help us choose directly adequate trial functions φn ( r) without any iteration. Inserting them in (44)then directly provides the energy.
to vary only slightly with the iteration order ( n ), in which case the Hartree-Fock equations have been solved to a good approximation. Using (44)we can then compute the energy we were looking for. It is also possible that physical arguments can help us choose directly adequate trial functions φn ( r) without any iteration. Inserting them in (44)then directly provides the energy.
Comments:
(i) The solutions of the Hartree-Fock equations may not be unique. Using the iteration process described above, one can easily wind up with different solutions, depending on the initial choice for the 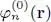 functions. This multiplicity of solutions is actually one of the method’s advantages, as it can help us find not only the ground level but also the excited levels.
functions. This multiplicity of solutions is actually one of the method’s advantages, as it can help us find not only the ground level but also the excited levels.
(ii) As we shall see in § 2, taking into account the 1/2 spin of the electrons in an atom does not bring major complications to the Hartree-Fock equations. It is generally assumed that the one-body potential is diagonal in a basis of the two spin states, labeled + and –, and that the interaction potential does not act on the spins. We then simply assemble N +equations, for N +wave functions  associated with the spin + particles, with N –other equations, for N –wave functions
associated with the spin + particles, with N –other equations, for N –wave functions 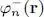 associated with spin — particles. These two sets of equations are not independent, since they contain the same direct potential (computed using (46), whose first line includes a summation over p of all the N = N ++ N _wave functions). As for the exchange potential, it does not lead to any coupling between the two sets of equations: in the second line of (46), the summation over p only includes particles in the same spin state for the following reason. If the particles have opposite spins, they can be recognized by the direction of their spin (the interaction does not act on the spins), and they no longer behave as indistinguishable particles. The exchange effects only arise for particles having the same spin.
associated with spin — particles. These two sets of equations are not independent, since they contain the same direct potential (computed using (46), whose first line includes a summation over p of all the N = N ++ N _wave functions). As for the exchange potential, it does not lead to any coupling between the two sets of equations: in the second line of (46), the summation over p only includes particles in the same spin state for the following reason. If the particles have opposite spins, they can be recognized by the direction of their spin (the interaction does not act on the spins), and they no longer behave as indistinguishable particles. The exchange effects only arise for particles having the same spin.
2. Generalization: operator method
We now describe the method in a more general way, using an operator method that leads to more concise expressions, while taking into account explicitly the possible existence of a spin – which plays an essential role in the atomic structure. We will identify more precisely the mathematical object, actually a projector, which we vary to optimize the energy. Physically, this projector is simply the one-particle density operator defined in § B-4 of Chapter XV. This will lead to expressions both more compact and general for the Hartree-Fock equations. They contain a Hartree-Fock operator acting on a single particle, as if it were alone, but which includes a potential operator defined by a partial trace which reflects the interactions with the other particles in the mean field approximation. Thanks to this operator we can get an approximate value of the entire system energy, computing only individual energies; these energies are obtained with calculations similar to the one used for a single particle placed in a mean field. With this approach, we have a better understanding of the way the mean field approximately represents the interaction with all the other particles; this approach can also suggest ways to make the approximations more precise.
Читать дальше

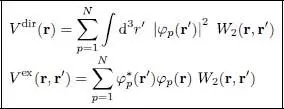
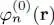 , and compute with (46)the associated potentials. Considering them to be fixed, we obtain linear eigenvalue equations which can be solved quite readily with computers (the single very complicated equation in a 3 N -dimensional space has been replaced by N independent 3-dimensional equations); we have to diagonalize a Hermitian operator to get a new series of orthonormal functions, resulting from the first iteration, and called
, and compute with (46)the associated potentials. Considering them to be fixed, we obtain linear eigenvalue equations which can be solved quite readily with computers (the single very complicated equation in a 3 N -dimensional space has been replaced by N independent 3-dimensional equations); we have to diagonalize a Hermitian operator to get a new series of orthonormal functions, resulting from the first iteration, and called 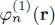 and
and 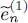 . The second iteration starts from these
. The second iteration starts from these 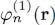 , to compute the new potential values, and get new linear differential equations. Solving these equations yields the next order
, to compute the new potential values, and get new linear differential equations. Solving these equations yields the next order 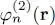 ,
, 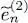 , etc. After a few iterations, one expects the
, etc. After a few iterations, one expects the 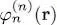 and
and 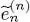 to vary only slightly with the iteration order ( n ), in which case the Hartree-Fock equations have been solved to a good approximation. Using (44)we can then compute the energy we were looking for. It is also possible that physical arguments can help us choose directly adequate trial functions φn ( r) without any iteration. Inserting them in (44)then directly provides the energy.
to vary only slightly with the iteration order ( n ), in which case the Hartree-Fock equations have been solved to a good approximation. Using (44)we can then compute the energy we were looking for. It is also possible that physical arguments can help us choose directly adequate trial functions φn ( r) without any iteration. Inserting them in (44)then directly provides the energy.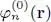 functions. This multiplicity of solutions is actually one of the method’s advantages, as it can help us find not only the ground level but also the excited levels.
functions. This multiplicity of solutions is actually one of the method’s advantages, as it can help us find not only the ground level but also the excited levels. associated with the spin + particles, with N –other equations, for N –wave functions
associated with the spin + particles, with N –other equations, for N –wave functions 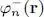 associated with spin — particles. These two sets of equations are not independent, since they contain the same direct potential (computed using (46), whose first line includes a summation over p of all the N = N ++ N _wave functions). As for the exchange potential, it does not lead to any coupling between the two sets of equations: in the second line of (46), the summation over p only includes particles in the same spin state for the following reason. If the particles have opposite spins, they can be recognized by the direction of their spin (the interaction does not act on the spins), and they no longer behave as indistinguishable particles. The exchange effects only arise for particles having the same spin.
associated with spin — particles. These two sets of equations are not independent, since they contain the same direct potential (computed using (46), whose first line includes a summation over p of all the N = N ++ N _wave functions). As for the exchange potential, it does not lead to any coupling between the two sets of equations: in the second line of (46), the summation over p only includes particles in the same spin state for the following reason. If the particles have opposite spins, they can be recognized by the direction of their spin (the interaction does not act on the spins), and they no longer behave as indistinguishable particles. The exchange effects only arise for particles having the same spin.










