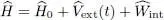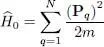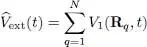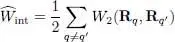Expressing the energy of the N -particle system as a function of ρI , we minimize it by varying this operator, and find the same results as above. This method amounts to a closure of the hierarchy of the N -body equations (§ C-4 of Chapter XVI). We have in fact already seen with equation (21)and in § 2-a that the Hartree-Fock approximation amounts to expressing the two-particle correlation functions as a function of the one-particle correlation functions. In terms of correlation functions (Complement A XVI), this amounts to replacing the two-particle function (four-point function) by a product of one-particle functions (two-point function), including an exchange term. Finally, another method is to use the diagram perturbation theory; the Hartree-Fock approximation corresponds to retaining only a certain class of diagrams (class of connected diagrams).
Finally note that the Hartree-Fock method is not the only one yielding approximate solutions of Schrodinger’s equation for a system of interacting fermions; in particular, one can use the “electronic density functional” theory (a functional is a function of another function, as for instance the action S in classical lagrangian mechanics). The method is used to obtain the electronic structure of molecules or condensed phases in physics, chemistry, and materials science. Its study nevertheless lies outside the scope of this book, and the reader is referred to [6], which summarizes the method and gives a number of references.
1 1 We assume the nucleus mass to be infinitely larger than the electron mass. The electronic system can then be studied assuming the nucleus fixed and placed at the origin.
2 2 The Pauli exclusion principle is not sufficient to explain why an atom’s size increases with its atomic number Z. One can evaluate the approximate size of a hypothetical atom with non-interacting electrons (we consider the atom’s size to be given by the size of the outermost occupied orbit). The Bohr radius a0 varies as 1/Z, whereas the highest value of the principal quantum number n of the occupied states varies approximately as Z1/3. The size n2a0 we are looking for varies approximately as Z-1/3.
3 3 As any Hermitian operator can be diagonalized, we simply show that (36)leads to matrix elements obeying the Hermitian conjugation relation. Let us verify that the two integrals and are complex conjugates of each other. For the contributions to these matrix elements of the kinetic and potential (in V1) energy, we simply find the usual relations insuring the corresponding operators are Hermitian. As for the interaction term, the complex conjugation is obvious for the direct term; for the exchange term, a simple inversion of the integral variables d3r and d3r′, plus the fact that W2(r, r′) is equal to W2(r′,r) allows verifying the conjugation.
4 4 A determinant value does not change if one adds to one of its column a linear combination of the others. Hence we can add to the first column of the Slater determinant (2)the linear combination of the θ2(r), θ3(r), … that makes it proportional to φ1(r). One can then add to the second column the combination that makes it proportional to φ2(r), etc. Step by step, we end up with a new expression for the original wave function , which now involves the Slater determinant of the φi(r). It is thus proportional to this determinant. A demonstration of the strict equality (within a phase factor) will be given in § 2.
5 5 As in the previous complement, we have replaced W2(R1, R2) by W2(1, 2) to simplify the notation
6 6 Since (71)shows that |δθ〉 is orthogonal to any linear combinations of the |θi〉, we can write (〈θj0| + 〈δθ|)(|θj0〉 + |δθ〉) = 〈θj0 |θj0〉 + 〈δθ |δθ〉 = 1 + second order terms.
7 7 The subscript k determines both the orbital and the spin state of the particle; the index ν is not independent since it is fixed for each value of k.
8 8 They all yield, however, an upper limit for the ground state energy
Complement F XVFermions, time-dependent Hartree-Fock approximation
1 1 Variational ket and notation
2 2 Variational method 2-a Definition of a functional 2-b Stationarity 2-c Particular case of a time-independent Hamiltonian
3 3 Computing the optimizer 3-a Average energy 3-b Hartree-Fock potential 3-c Time derivative 3-d Functional value
4 4 Equations of motion 4-a Time-dependent Hartree-Fock equations 4-b Particles in a single spin state 4-c Discussion
The Hartree-Fock mean field method was introduced in Complement E XVfor a time-independent problem: the search for the stationary states of a system of interacting fermions (the search for its thermal equilibrium will be discussed in Complement G XV. In this complement, we show how this method can be used for time-dependent problems. We start, in § 1, by including a time dependence in the Hartree-Fock variational ket (time-dependent Fock state). We then introduce in § 2 a general variational principle that can be used for solving the time-dependent Schrödinger equation. We then compute, in § 3, the function to be optimized for a Fock state; the same mean field operator as the one introduced in Complement E XVwill here again play a very useful role. Finally, the time-dependent Hartree-Fock equations will be obtained and discussed in § 4. More details on the Hartree-Fock methods in general can be found, for example, in Chapter 7 of reference [5], and especially in its Chapter 9 for time-dependent problems.
1. Variational ket and notation
We assume the N -particle state vector  to be of the form:
to be of the form:
(1) 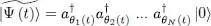
where the 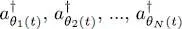 are the creation operators associated with an arbitrary series of orthonormal individual states | θ 1( t )〉, | θ 2( t )〉, …, | θN ( t )〉 which depend on time t . This series is, for the moment, arbitrary, but the aim of the following variational calculation is to determine its time dependence.
are the creation operators associated with an arbitrary series of orthonormal individual states | θ 1( t )〉, | θ 2( t )〉, …, | θN ( t )〉 which depend on time t . This series is, for the moment, arbitrary, but the aim of the following variational calculation is to determine its time dependence.
As in the previous complements, we assume that the Hamiltonian Ĥ is the sum of three terms: a kinetic energy Hamiltonian, an external potential Hamiltonian, and a particle interaction term:
(2) 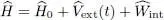
with:
(3) 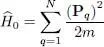
(m is the particles’ mass, P qthe momentum operator of particle q ), and:
(4) 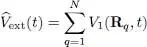
and finally:
(5) 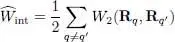
Читать дальше

 to be of the form:
to be of the form: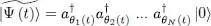
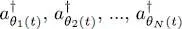 are the creation operators associated with an arbitrary series of orthonormal individual states | θ 1( t )〉, | θ 2( t )〉, …, | θN ( t )〉 which depend on time t . This series is, for the moment, arbitrary, but the aim of the following variational calculation is to determine its time dependence.
are the creation operators associated with an arbitrary series of orthonormal individual states | θ 1( t )〉, | θ 2( t )〉, …, | θN ( t )〉 which depend on time t . This series is, for the moment, arbitrary, but the aim of the following variational calculation is to determine its time dependence.