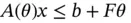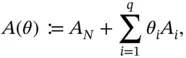Efstratios N. Pistikopoulos - Multi-parametric Optimization and Control

(2.22a)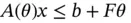

(2.22b)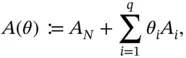

where algorithms based on McCormick relaxations [33,34], as well as exact algorithms for the single parameter case [35] have been presented. 6

1 1 Spjøtvold, J., Tøndel, P., and Johansen, T.A. (2005) A method for obtaining continuous solutions to multiparametric linear programs, in World Congress, IFAC, Elsevier, IFAC proceedings volumes, p. 902, doi: 0703‐6‐CZ‐1902.00903.

2 2 Gal, T. and Nedoma, J. (1972) Multiparametric linear programming. Management Science, 18 (7), 406–422, doi: 10.1287/mnsc.18.7.406.

3 3 Olaru, S. and Dumur, D. (2006) On the continuity and complexity of control laws based on multiparametric linear programs, in 45th IEEE Conference on Decision and Control, 2006, pp. 5465–5470, doi: 10.1109/CDC.2006.377330.

4 4 Jones, C.N., Kerrigan, E.C., and Maciejowski, J.M. (2007) Lexicographic perturbation for multiparametric linear programming with applications to control. Automatica, 43 (10), 1808–1816, doi: 10.1016/j.automatica.2007.03.008. URL http://www.sciencedirect.com/science/article/pii/S0005109807002002.

5 5 Hladík, M. (2010) Multiparametric linear programming: support set and optimal partition invariancy. European Journal of Operational Research, 202 (1), 25–31, doi: 10.1016/j.ejor.2009.04.019. URL http://www.sciencedirect.com/science/article/pii/S0377221709002926.

6 6 Gal, T. and Greenberg, H.J. (1997) Advances in sensitivity analysis and parametric programming, vol. 6, Springer US, Boston, MA, doi: 10.1007/978‐1‐4615‐6103‐3.

7 7 Hadigheh, A.G. and Terlaky, T. (2006) Generalized support set invariancy sensitivity analysis in linear optimization. Journal of Industrial and Management Optimization, 2 (1), 1–18.

8 8 Hadigheh, A.G. and Terlaky, T. (2006) Sensitivity analysis in linear optimization: invariant support set intervals. European Journal of Operational Research, 169 (3), 1158–1175, doi: 10.1016/j.ejor.2004.09.058. URL http://www.sciencedirect.com/science/article/pii/S0377221705002808.

9 9 Hadigheh, A.G., Mirnia, K., and Terlaky, T. (2007) Active constraint set invariancy sensitivity analysis in linear optimization. Journal of Optimization Theory and Applications, 133 (3), 303–315, doi: 10.1007/s10957‐007‐9201‐5. URL http://dx.doi.org/10.1007/s10957-007-9201-5.

10 10 Greenberg, H.J. (1994) The use of the optimal partition in a linear programming solution for postoptimal analysis. Operations Research Letters, 15 (4), 179–185, doi: 10.1016/0167‐6377(94)90075‐2. URL http://www.sciencedirect.com/science/article/pii/0167637794900752.

11 11 Berkelaar, A.B., Roos, K., and Terlaky, T. (1997) The optimal set and optimal partition approach to linear and quadratic programming, in (eds T. Gal and H.J. Greenberg) Advances in sensitivity analysis and parametic programming, Springer US, Boston, MA, pp. 159–202, doi: 10.1007/978‐1‐4615‐6103‐3_6. URL http://dx.doi.org/10.1007/978-1-4615-6103-3_6.

12 12 Greenberg, H.J. (2000) Simultaneous primal‐dual right‐hand‐side sensitivity analysis from a strictly complementary solution of a linear program. SIAM Journal on Optimization, 10 (2), 427–442, doi: 10.1137/S1052623496310333. URL http://dx.doi.org/10.1137/S1052623496310333.

13 13 Dantzig, G.B. (1963) Linear programming and extensions, Princeton University Press, Princeton, NJ.

14 14 Gal, T. (1985) The historical development of parametric programming, in Parametric optimization and approximation, International series of numerical mathematics / Internationale Schriftenreihe zur Numerischen Mathematik / Série internationale d'Analyse numérique, vol. 72 (eds B. Brosowski and F. Deutsch), Birkhäuser Verlag, Basel, pp. 148–165, doi: 10.1007/978‐3‐0348‐6253‐0_10. URL http://dx.doi.org/10.1007/978-3-0348-6253-0_10.

15 15 Manne, A.S. (1953) Notes on parametric linear programming, RAND Corporation, pp. P–468. URL http://www.rand.org/pubs/papers/P468.

16 16 Gass, S. and Saaty, T. (1955) The computational algorithm for the parametric objective function. Naval Research Logistics Quarterly, 2 (1–2), 39–45, doi: 10.1002/nav.3800020106. URL http://dx.doi.org/10.1002/nav.3800020106.

17 17 Orchard‐Hays, W. (1955) The RAND code for the simplex method (SX4): (For the IBM 701 electronic computer), Rand Corporation, Santa Monica, CA.

18 18 Saaty, T.L. (1959) Coefficient perturbation of a constrained extremum. Operations Research, 7 (3), 294–302, doi: 10.1287/opre.7.3.294. URL http://dx.doi.org/10.1287/opre.7.3.294.

19 19 Simons, E. (1962) A note on parametric linear programming. Management Science, 8 (3), 355–358, doi: 10.1287/mnsc.8.3.355. URL http://dx.doi.org/10.1287/mnsc.8.3.355.

20 20 Karabegov, V.K. (1963) A parametric problem in linear programming. USSR Computational Mathematics and Mathematical Physics, 3 (3), 725–741, doi: 10.1016/0041‐5553(63)90297‐0. URL http://www.sciencedirect.com/science/article/pii/0041555363902970.

21 21 Gal, T. and Davis, G.V. (1978, cop. 1979) Postoptimal analyses, parametric programming and related topics, McGraw‐Hill, London.

22 22 Gál, T. (1995) Postoptimal analyses, parametric programming, and related topics: degeneracy, multicriteria decision making, redundancy, W. de Gruyter, Berlin and New York, 2nd edn.

23 23 Acevedo, J. and Pistikopoulos, E.N. (1997) A multiparametric programming approach for linear process engineering problems under uncertainty. Industrial and Engineering Chemistry Research, 36 (3), 717–728, doi: 10.1021/ie960451l.

24 24 Dua, V. and Pistikopoulos, E.N. (1999) Algorithms for the solution of multiparametric mixed‐integer nonlinear optimization problems. Industrial and Engineering Chemistry Research, 38 (10), 3976–3987, doi: 10.1021/ie980792u.

25 25 Dinkelbach, W. (1969) Sensitivitätsanalysen und parametrische Programmierung, Ökonometrie und Unternehmensforschung / Econometrics and Operations Research, vol. 12, Springer‐Verlag, Berlin, Heidelberg.

26 26 Bemporad, A., Morari, M., Dua, V., and Pistikopoulos, E.N. (2000) The explicit solution of model predictive control via multiparametric quadratic programming. Proceedings of the American Control Conference, vol. 2, pp. 872–876, doi: 10.1109/ACC.2000.876624.

27 27 Bemporad, A., Morari, M., Dua, V., and Pistikopoulos, E.N. (2002) The explicit linear quadratic regulator for constrained systems. Automatica, 38 (1), 3–20, doi: 10.1016/S0005‐1098(01)00174‐1. URL http://www.sciencedirect.com/science/article/pii/S0005109801001741.

28 28 Bemporad, A., Borrelli, F., and Morari, M. (2002) Model predictive control based on linear programming ‐ the explicit solution. IEEE Transactions on Automatic Control, 47 (12), 1974–1985, doi: 10.1109/TAC.2002.805688.

29 29 Bemporad, A., Borrelli, F., and Morari, M. (2000) The explicit solution of constrained LP‐based receding horizon control, in Proceedings of the 39th IEEE Conference on Decision and Control, 2000, vol. 1, pp. 632–637, doi: 10.1109/CDC.2000.912837.

30 30 Borrelli, F., Bemporad, A., and Morari, M. (2003) Geometric algorithm for multiparametric linear programming. Journal of Optimization Theory and Applications, 118 (3), 515–540, doi: 10.1023/B:JOTA.0000004869.66331.5c. URL URL http://dx.doi.org/10.1023/B%3AJOTA.0000004869.66331.5c.

31 31 Morari, M., Jones, C.N., Zeilinger, M.N., and Baric, M. (2008) Multiparametric linear programming for control, in CCC 2008. 27th Chinese Control Conference, 2008, pp. 2–4, doi: 10.1109/CHICC.2008.4604876.