1 Cover
2 Title Page Digital Sciences Set coordinated by Abdelkhalak El Hami Volume 1
3 Copyright First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2021 The rights of Abdelkhalak El Hami and Bouchaib Radi to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2020948478 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-84821-953-3
4 Preface
Acknowledgments Acknowledgments We would like to thank everyone who contributed, directly or indirectly, to the writing of this book and especially, the engineering and PhD students of INSA Rouen whom we have had the pleasure of supervising over the past few years. Bouchaib RADI Abdelkhalak EL HAMI November 2020
5 PART 1: Programmation
1 Linear Programming
1.1. Introduction 1.2. Definitions 1.2. Definitions DEFINITION 1.1.– An LP is in canonical form if it is expressed as follows: [1.1] An LP is in standard form if it is expressed as follows: Every linear problem can be expressed in canonical form: min cTx = – max cTx. THEOREM 1.1.– Every LP in standard form can be expressed in canonical form and vice versa.
1.3. Geometry of the linear program 1.3. Geometry of the linear program 1.3.1. Polyhedra DEFINITION 1.2.– A polyhedron is a set that can be described as where A is an m × n matrix and b is a vector in ℝ m . Note that the admissible set of an LP is a polyhedron. DEFINITION 1.3.– A polyhedron P is said to be bounded if there exists a constant c such that || x || ≤ c for every x ∈ P . Figure 1.1. Bounded polyhedron (left) and unbounded polyhedron (right). For a color version of this figure, see www.iste.co.uk/radi/optimizations.zip DEFINITION 1.4.– Let a be a non-zero vector of ℝ n , and let b be a scalar. – The set {x ∈ ℝn|aTx = b} is said to be a hyperplane. – The set {x ∈ ℝn|aTx ≥ b} is said to be a half-space. Note that a hyperplane is the boundary of the corresponding half-space and the vector a is perpendicular to the hyperplane that it defines [TEG 12].
1.4. Graphical solving of a linear program 1.5. Simplex algorithm 1.6. Initialization of the simplex algorithm 1.7. Interior-point algorithm 1.8. Duality 1.9. Relaxation 1.10. Postoptimal analysis 1.11. Application to an inventory problem 1.12. Using Matlab 2 Integer Programming2.1. Introduction 2.2. Solving methods 2.3. Binary programming 2.4. Decomposition principle 2.5. Using Matlab 3 Dynamic Programming3.1. Introduction 3.2. Solving strategy 3.3. Discrete DP 3.4. Continuous DP 3.5. Stochastic DP 3.6. Using Matlab 4 Stochastic Programming4.1. Introduction 4.2. Presentation of the problem 4.3. Optimal feedback in an open loop 4.4. Stochastic linear programming 4.5. Stochastic linear programs with recourse 4.6. Nonlinear stochastic programming 4.7. Stochastic dynamic programming 4.8. Application to the reliability of mechanical systems 4.9. Using Matlab
6 PART 2: Optimization 5 Combinatorial Optimization5.1. Introduction 5.2. Symmetric TSP 5.3. Asymmetric traveling salesman problem 5.4. Vehicle routing problem 5.5. Selective routing problem 5.6. Using Matlab 6 Unconstrained Nonlinear Programming6.1. Introduction 6.2. Mathematical formulation 6.3. Optimality conditions 6.4. Quadratic problems 6.5. Newton’s algorithm 6.6. Methods of descent and linear search 6.7. Quasi-Newton methods 6.8. Relaxation method 6.9. Gradient method 6.10. Least squares problem 6.11. Direct search methods 6.12. Application to an identification problem 6.13. Using Matlab 7 Constrained Nonlinear Optimization7.1. Introduction 7.2. Mathematical formulation 7.3. Lagrange multipliers 7.4. Optimization with inequality constraints 7.5. Constrained minimization algorithms 7.6. Newton algorithms: SQP method 7.7. Application to structure optimization 7.8. Using Matlab
7 Appendices Appendix 1: Reminders from Linear Algebra A1.1. Vector space A1.2. Linear mappings A1.3. Matrices A1.4. Determinants A1.5. Scalar product A1.6. Vector norm Appendix 2: Reminders about functions from ℝ n into ℝ A2.1. Differentiability A2.2. Convexity A2.3. Quadratic function Appendix 3: Optimization ToolboxA3.1. Introduction A3.2. Various functions A3.3. Matlab’s optimization application Appendix 4: SoftwareA4.1. Autonomous and multipurpose optimization software A4.2. Packages for specific classes of problems A4.3. Optimization software for design A4.4. Solvers for stochastic optimization
8 References
9 Index
10 End User License Agreement
1 Chapter 1 Table 1.1. First simplex tableau Table 1.2. Second simplex tableau 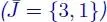 Table 1.3. Third simplex tableau
Table 1.3. Third simplex tableau 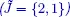
2 Chapter 3Table 3.1. Table constructed to solve the problemTable 3.2. List of n objectsTable 3.3. Results of the recursive formulaTable 3.4. Demand and purchase pricesTable 3.5. Solution of the stock problem
3 Chapter 4Table 4.1. Characteristics of the random variables for the concrete beamTable 4.2. Results obtained with the FORM method for the concrete beam
4 Chapter 6Table 6.1. Material properties
5 Chapter 7Table 7.1. Results calculated with MatlabTable 7.2. Solution calculated with Matlab
6 Appendix 3Table A3.1. Optimization problems supported by the optimization toolbox
1 Chapter 1 Figure 1.1. Bounded polyhedron (left) and unbounded polyhedron (right). For a co... Figure 1.2. Graphical solution. For a color version of this figure, see www.iste... Figure 1.3. Graphical solution with isoprofit lines. For a color version of this...
2 Chapter 2 Figure 2.1. Branch-and-bound method Figure 2.2. Branch-and-cut methodFigure 2.3. Matrix A
3 Chapter 3Figure 3.1. Different cities. For a color version of this figure, see www.iste.c...Figure 3.2. DAG representing the dependencies between the different subproblems ...Figure 3.3. Level-dependent multilevel DAG for the shortest path problem. For a ...Figure 3.4. Level-independent multilevel DAG for the shortest path problem. For ...Figure 3.5. Graph corresponding to this problemFigure 3.6. Graph constructed from this problemFigure 3.7. Decision-chance tree for the insurance contract problem. For a color...Figure 3.8. Binary search tree for set A. For a color version of this figure, se...Figure 3.9. Five possible binary trees for list S. For a color version of this f...
4 Chapter 4Figure 4.1. Constructing a scenario tree. For a color version of this figure, se...Figure 4.2. Example of a tree structure. For a color version of this figure, see...Figure 4.3. Geometric representation of β HLfor a problem with two random variab...Figure 4.4. Most probable failure point. For a color version of this figure, see...Figure 4.5. Illustration of FORM. For a color version of this figure, see www.is...Figure 4.6. Diagram of the beam on simple supports of reinforced concrete
Читать дальше

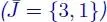 Table 1.3. Third simplex tableau
Table 1.3. Third simplex tableau