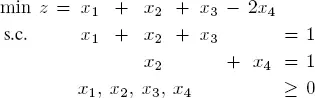REMARK.– For a comprehensive discussion of the efficiency of the simplex method, refer to [CHV 83].
1.6. Initialization of the simplex algorithm
This section presents two techniques for finding a basic realizable solution to initialize the simplex algorithm: the first is the Big M method, and the second is the Phase I method.
Suppose that we wish to solve the LP
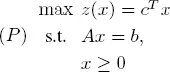
where A is an m × n matrix, rank A = m < n .
By adding slack variables (with positive or negative signs), we can always reduce the LP to the form (P) described above, with 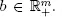 If there is no obvious basic realizable solution to initialize the simplex algorithm, we proceed by adding artificial variables yi ≥ 0 to the constraints:
If there is no obvious basic realizable solution to initialize the simplex algorithm, we proceed by adding artificial variables yi ≥ 0 to the constraints:
Ax = b is replaced by Ax + y = b , y = ( y 1, y 2, . . . , ym ) T ∈ 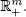
The new constraints are not equivalent to the initial constraints. The yi > 0 are penalized by replacing the objective function z ( x ) with
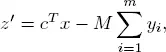
where M is some very large positive value. We will choose yi = bi , i = 1, . . . , m , as a basic feasible solution to serve as the initial solution.
Since the yi significantly reduce the value of z ′, they will disappear from the basis over the course of the simplex algorithm. As they are non-basic variables, their value will be equal to zero, and the LP that is ultimately solved is the same as the program (P).
EXAMPLE 1.7.– Consider the LP
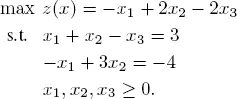
The new program is given as
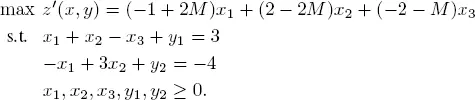
The first tableau is as follows:
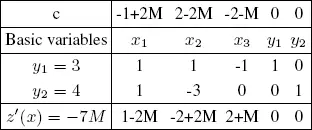
The second tableau is as follows:
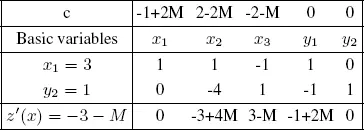
The third tableau is as follows:
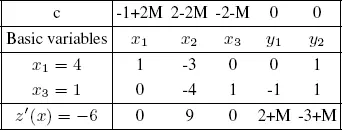
The unique optimal solution is given by x 1= 4, x 2= 0, x 3= 1, and z ( x 1, x 2, x 3) = −6.
1.6.2. Auxiliary program or Phase I
Suppose that the LP that we wish to solve is in the standard form:
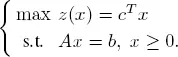
The auxiliary program method proceeds by letting M → +∞ in ( PM ) and solving the program obtained in the limit. Let

Maximizing z ′( x, y ) is equivalent to maximizing z ″ ( x, y ), or maximizing
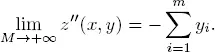
We therefore solve the auxiliary program ( PA ) given by
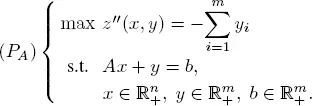
The simplex algorithm can now be applied to ( PA ) starting from the basic realizable solution y = b.
– First case: max z″ (y) < 0. There exists yi > 0, i ∈ {1, 2, . . . , m}. In this case, (P ) does not have any realizable solutions.
– Second case: max z″ (y) = 0. The optimal solution of (PA) can be used as an initial basic realizable solution for applying the simplex algorithm to (P ). The objective function of (P ) is expressed in terms of non-basic variables, then the simplex algorithm is applied to (P ).
REMARK.– For a minimization problem, we add 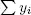 instead.
instead.
Let us go into more detail for a minimization problem. The initial tableau of the auxiliary problem is as follows:

where B = I , cB = (1, 1, 1, . . .) T , and the matrices A and b relate to the auxiliary program. For the original variables i, we have ci = 0.
If ( x *, y *) is a zero-cost optimal solution of the auxiliary problem, then the artificial variable in the basis is necessarily zero, so the solution is degenerate.
If we assume that the k th basic variable is artificial, consider the k th row of the tableau and select the element of this row in column j , where j is the index of a variable in the original problem. If the element is non-zero: k leaves the basis and j enters the basis, and we pivot the tableau. But what if no such element exists? This would mean that the matrix A does not have full rank, and the row in question corresponds to a redundant constraint.
Once the optimal tableau of the auxiliary problem has been obtained and all artificial variables have left the basis, we obtain the initial tableau of the original problem P1 by deleting any columns that relate to the artificial variables and calculating the reduced initial costs: 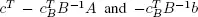 in the box reserved for the cost function. The following example shows how this method works.
in the box reserved for the cost function. The following example shows how this method works.
EXAMPLE 1.8.– Consider the following linear programming problem:
[1.10] 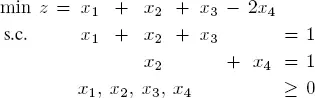
Читать дальше

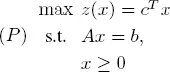
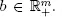 If there is no obvious basic realizable solution to initialize the simplex algorithm, we proceed by adding artificial variables yi ≥ 0 to the constraints:
If there is no obvious basic realizable solution to initialize the simplex algorithm, we proceed by adding artificial variables yi ≥ 0 to the constraints: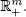
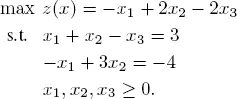
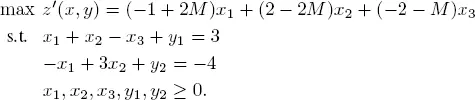



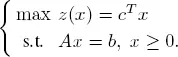

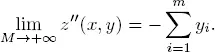
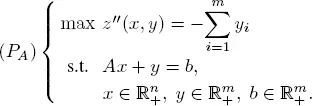
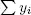 instead.
instead.
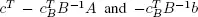 in the box reserved for the cost function. The following example shows how this method works.
in the box reserved for the cost function. The following example shows how this method works.