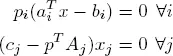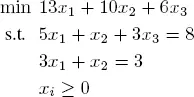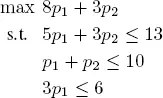Duality is an essential notion in linear programming. The duality operation associates any so-called primal linear programming problem with another such problem, known as the dual, that is defined solely in terms of the data of the primal problem.
Duality is interesting for two reasons:
– the dual problem has an important economic interpretation that offers another perspective of the primal problem;
– there are straightforward and powerful mathematical relations between the primal and dual problems; this will allow us to develop new algorithms that will be more efficient in many situations.
Suppose that we have the following primal program:
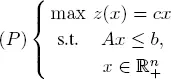
Its dual program is as follows:
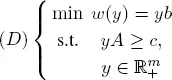
REMARK.– The primal and dual programs satisfy the following relations:
– m = number of constraints of (P) = number of variables of (D),
– n = number of variables of (P) = number of constraints of (D).
If ( P ) has two constraints, ( D ) has two variables and can be solved graphically, regardless of the number of variables of ( P ).
So, what is the form of ( D ) when ( P ) is not in canonical form?
In such a case, we can determine ( D ) by reducing ( P ) to canonical form, as shown in the following example.
EXAMPLE 1.10.– Consider the LP:
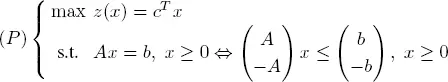
By the above definition, the dual of ( P ) is given by
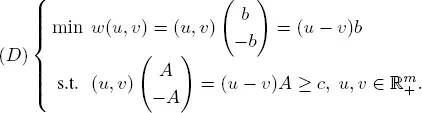
Setting y = u − v gives
( D ) min w ( y ) = yb s.t. yA ≥ c , y with no sign restriction (denoted ( y )).
In general, we have:

THEOREM 1.8.– The dual of the dual is the primal.
Now that we have defined the dual of a linear program, let us study the links between the solutions of programs that are dual to one another.
THEOREM 1.9.– Let ( x , y ) be a feasible solution of ( 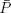 ) and ( u , v ) a feasible solution of (
) and ( u , v ) a feasible solution of ( 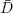 ). Then:
). Then:
1) z(x, y) ≤ w(u, v);
2) z(x, y) = w(u, v) ⇒ (x, y) and (u, v) are optimal solutions of () and ( ).
THEOREM 1.10.– One of the following three cases is satisfied:
1) () and () have optimal solutions and max z(x, y) = min w(u, v);
2) one of () and () has a feasible solution, but not the other;
3) neither () nor () have feasible solutions.
THEOREM 1.11.– Let ( x , y ) (respectively, ( u , v )) be feasible solutions of ( 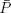 ) (respectively, (
) (respectively, ( 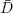 )). Then ( x , y ) and ( u , v ) are optimal solutions of (
)). Then ( x , y ) and ( u , v ) are optimal solutions of ( 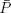 ) and (
) and ( 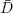 ) if and only if the following statements hold:
) if and only if the following statements hold:
– if one constraint is strictly an inequality in () (respectively, ()), then the corresponding variable of () (respectively, of ()) is zero;
– if the value of a restricted variable (i.e. a positive variable or a negative variable) in one of the programs () or () is not zero, then the corresponding constraint in the other program is an equality.
This theorem can alternatively be stated as follows:
THEOREM 1.12.– Let x and p be admissible solutions of the primal and dual programs, respectively. Then the vectors x and p are, respectively, optimal solutions of the two problems if and only if:
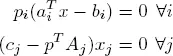
Consider the LP
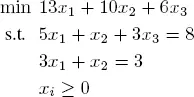
The dual of this program is:
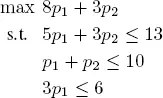
The solution of the primal is x * = (1, 0, 1) T .
The optimal dual solution can be constructed from additional slack conditions:
– the condition = 0 is satisfied because x* is admissible;
– the condition (cj − pT Aj)xj = 0 is satisfied for j = 2:- for j = 1, this condition becomes:5p1 + 3p2 = 13.- for j = 3, it becomes:3p1 = 6.
These two conditions give p 1= 2 and p 2= 1. This solution is dual admissible. The total dual cost is 19, and so is the primal cost.
In mathematical programming, good performance essentially depends on the program’s ability to construct useful bounds (lower bounds for maximization and upper bounds for minimization). These bounds can be obtained by relaxing the linear program, i.e.
– either increasing the set of solutions to optimize over a larger space (that is easier to optimize); this includes constraint relaxation (and in particular continuous relaxation);
– or replacing the objective function with an upper bound (in the case of maximization), for example, Lagrangian relaxation.
For a mathematical program, the following continuous relaxations are possible:
– (simple) continuous maximization, which is very effective for LPs (with the simplex algorithm, the interior-point method, or the volume algorithm); however, we will see that continuous relaxation is rarely the best option;
– in the specific context of LPs, we can improve the value of linear relaxation by adding constraints – reinforcement;
– we can also add variables – reformulation;
– Lagrangian relaxation is another approach.
1.9.1. Lagrangian relaxation
Lagrangian duality provides a particularly fruitful framework for relaxation. It works as follows:
– choose an inequality in the LP and remove it from the LP;
– add this inequality to the objective function with a multiplier that penalizes the objective function if the solution found does not satisfy the inequality.
Читать дальше

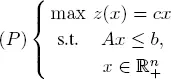
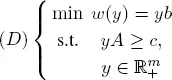
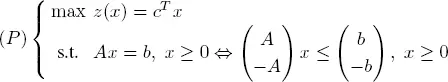
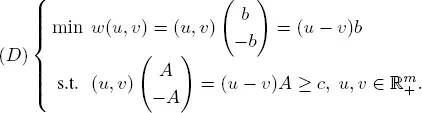

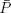 ) and ( u , v ) a feasible solution of (
) and ( u , v ) a feasible solution of ( 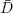 ). Then:
). Then: