Efstratios N. Pistikopoulos - Multi-parametric Optimization and Control
Здесь есть возможность читать онлайн «Efstratios N. Pistikopoulos - Multi-parametric Optimization and Control» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Multi-parametric Optimization and Control
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Multi-parametric Optimization and Control: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Multi-parametric Optimization and Control»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
ecent developments in multi-parametric optimization and control
Multi-Parametric Optimization and Control Researchers and practitioners can use the book as reference. It is also suitable as a primary or a supplementary textbook. Each chapter looks at the theories related to a topic along with a relevant case study. Topic complexity increases gradually as readers progress through the chapters. The first part of the book presents an overview of the state-of-the-art multi-parametric optimization theory and algorithms in multi-parametric programming. The second examines the connection between multi-parametric programming and model-predictive control—from the linear quadratic regulator over hybrid systems to periodic systems and robust control.
The third part of the book addresses multi-parametric optimization in process systems engineering. A step-by-step procedure is introduced for embedding the programming within the system engineering, which leads the reader into the topic of the PAROC framework and software platform. PAROC is an integrated framework and platform for the optimization and advanced model-based control of process systems.
Uses case studies to illustrate real-world applications for a better understanding of the concepts presented Covers the fundamentals of optimization and model predictive control Provides information on key topics, such as the basic sensitivity theorem, linear programming, quadratic programming, mixed-integer linear programming, optimal control of continuous systems, and multi-parametric optimal control An appendix summarizes the history of multi-parametric optimization algorithms. It also covers the use of the parametric optimization toolbox (POP), which is comprehensive software for efficiently solving multi-parametric programming problems.

 will be less than or equal to the feasible solution, i.e.
will be less than or equal to the feasible solution, i.e. 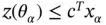 and thus:
and thus: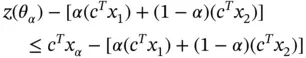
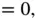
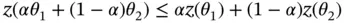 ,
, 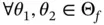 ,
, 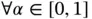 . This proves the convexity of
. This proves the convexity of  and
and 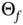 . The piecewise affine nature of
. The piecewise affine nature of 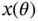 and
and 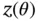 is a direct result from the fact that the boundary between two regions belongs to both regions. Since the optimum is unique, the optimizer and thus the optimal objective function value must be continuous across the boundary.
is a direct result from the fact that the boundary between two regions belongs to both regions. Since the optimum is unique, the optimizer and thus the optimal objective function value must be continuous across the boundary.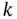 of an mp‐LP problem be a node in the set of solutions
of an mp‐LP problem be a node in the set of solutions 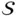 . Then the nodes
. Then the nodes 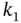 and
and 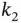 are connected if (i) there exists a
are connected if (i) there exists a 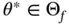 such that
such that 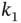 and
and 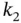 are both optimal active sets and (ii) it is possible to pass from
are both optimal active sets and (ii) it is possible to pass from 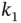 to
to 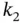 by one step of the dual simplex algorithm. The resulting graph
by one step of the dual simplex algorithm. The resulting graph 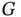 is fully defined by the nodes
is fully defined by the nodes 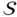 as well as all connections
as well as all connections  , i.e.
, i.e. 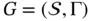 .
.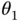 ,
, 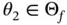 be two arbitrary feasible parameters and
be two arbitrary feasible parameters and 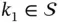 be given such that
be given such that 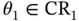 . Then there exists a path
. Then there exists a path  in the mp‐LP graph
in the mp‐LP graph 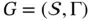 such that
such that  .
.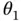 and
and 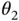 , i.e.
, i.e.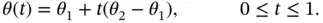
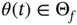 , as
, as 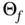 is convex. Setting
is convex. Setting 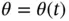 in the mp‐LP problem ( 2.2) converts the original mp‐LP problem into a parametric linear programming (p‐LP) problem. The solution of this p‐LP problem is given by a series of line segments that are connected as the union constitutes the feasible parameter space
in the mp‐LP problem ( 2.2) converts the original mp‐LP problem into a parametric linear programming (p‐LP) problem. The solution of this p‐LP problem is given by a series of line segments that are connected as the union constitutes the feasible parameter space 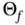 and is convex based on Theorem 2.1. Based on Eq. (2.6), the limits of each line segment result from the violation of a currently inactive constraint for the parametric solution of that line segment, as all the active constraints are satisfied by definition. Thus, in order to move beyond these limits, the violated constraint needs to be considered as an active constraint, i.e. a step of the dual simplex algorithm needs to be performed. This results in a new active set, and by extension in a sequence of active sets that correspond to the path
and is convex based on Theorem 2.1. Based on Eq. (2.6), the limits of each line segment result from the violation of a currently inactive constraint for the parametric solution of that line segment, as all the active constraints are satisfied by definition. Thus, in order to move beyond these limits, the violated constraint needs to be considered as an active constraint, i.e. a step of the dual simplex algorithm needs to be performed. This results in a new active set, and by extension in a sequence of active sets that correspond to the path  in the mp‐LP graph
in the mp‐LP graph 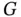 .
.










