Efstratios N. Pistikopoulos - Multi-parametric Optimization and Control

Figure 2.2shows some of the properties of the solution of the mpLP problem 2.2.

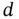Note that it is possible to add a scalar to the objective function of an LP problem without influencing the optimal solution. Similarly, it is possible to add an arbitrary scaling function 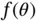to an mp‐LP problem without influencing the optimal solution.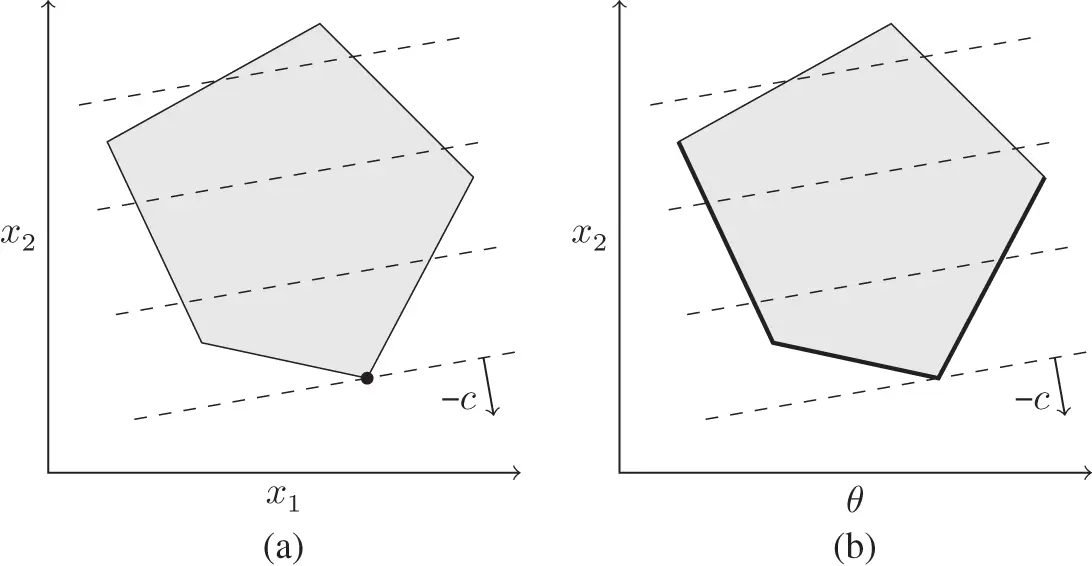

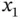Figure 2.1The difference between the solution of an LP and an mp‐LP problem (black dot and line, respectively), where the mp‐LP problem is obtained by treating as a parameter. In (a), the solution is a single point in one of the vertices of the feasible space, while in (b) the solution is a function of the parameter .

Due to the similarities between mp‐LP and multi‐parametric quadratic programming (mp-QP) problems, the different solution strategies available are discussed in detail in Chapter 4.

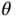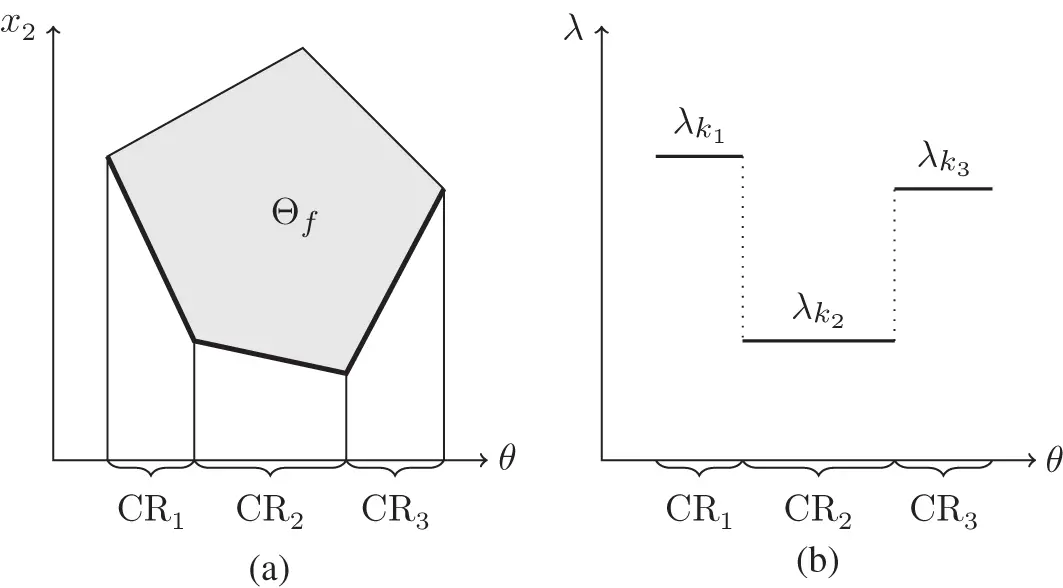
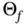Figure 2.2A schematic representation of the solution of the mp‐LP problem from Figure 2.1. In (a), the partitioning of the convex, feasible parameter space , as well as the piecewise affine nature of the optimal solution 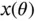and the convex and piecewise affine nature of the objective function 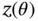is shown. In (b), the Lagrange multipliers 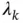as a function of 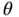are shown.

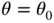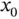Consider a fixed, nominal point , which transforms the mp‐LP problem ( 2.2) into an LP problem of type ( 2.1). The solution of this LP problem at yields the solution as well as the values of the Lagrange multipliers 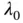. Based on these, the indices of the active set 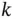are identified: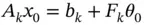

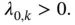
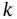(2.3a)

(2.3b)

In the case where the set from Eq. (2.3) is not unique, the solution is said to be degenerate. The impact of degeneracy on the parametric solution is discussed in Chapter 2.2.

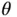Together with the equality constraints, which have to be satisfied for any , the following active set matrices and vectors are defined: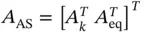

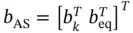
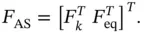
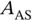(2.4a)

(2.4b)

(2.4c)

Note that has to have full rank in order to fulfill the LICQ condition described in Chapter 1. Since the objective function is linear and the constraints are affine, the change of the solution of problem ( 2.2) based on the basic sensitivity theorem is given by 2: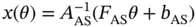

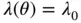
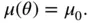
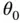(2.5a)

(2.5b)

(2.5c)

Based on Eq. (2.5), the following statements regarding the solution around can be made:

The optimization variables are affine functions of the parameter .

In the case of mp‐LP problems, the values of the Lagrange multipliers and do not change as a function of around a nominal point .

The square matrix is invertible since the SCS and LICQ conditions of Chapter 1have to hold.

In order for Eq. (2.5) to remain the optimal solution around a nominal point , it needs to be feasible, i.e.(2.6a) (2.6b) Note that since the values of the Lagrange multipliers do not change as a function of , the optimality requirement from the Karush‐Kuhn‐Tucker conditions can be omitted from the construction of the feasible region.

Thus, the optimal solution of problem ( 2.2) around is given by Eq. (2.5) and is valid in the compact polytope described by Eq. (2.6), which is referred to as critical region :