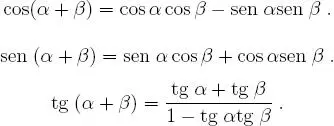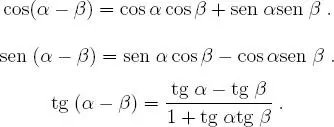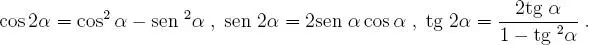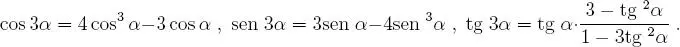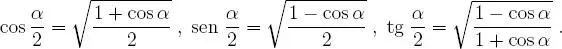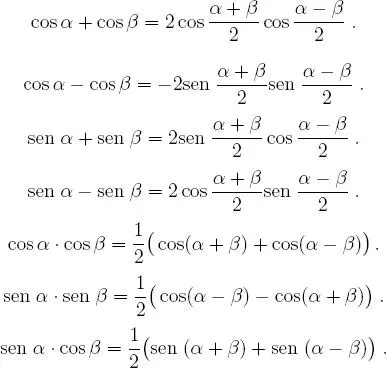
1.3Expresión de cada razón trigonométrica en términos de las restantes
Ocupando las identidades fundamentales dadas en el teorema [1.1.1] se obtiene el cuadro siguiente:
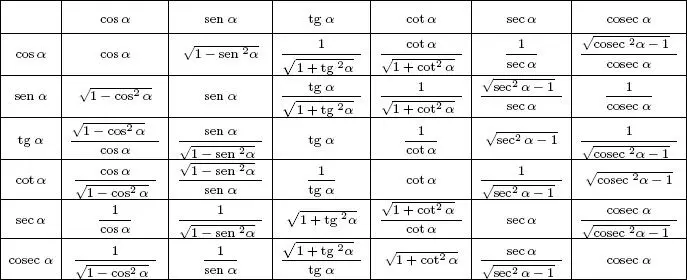
1.4Resolución de triángulos rectángulos
Los criterios de congruencia de triángulos, en el caso en que tales triángulos sean rectángulos, nos indican que un triángulo rectángulo quedará determinado dándose dos datos, dentro de los cuales debe haber por lo menos uno que sea lineal (o sea, un lado). Luego, para que un triángulo rectángulo quede determinado bastará considerar alguna de las cinco situaciones siguientes:
(1)Hipotenusa y ángulo agudo.
(2)Cateto y ángulo agudo adyacente.
(3)Cateto y ángulo agudo opuesto.
(4)Cateto y cateto.
(5)Cateto e hipotenusa.
Para resumir estos cinco casos consideraremos la figura 1.2.
Caso N ◦ 1:Observando la figura 1.2, donde los datos son la hipotenusa AB = c y el ángulo agudo ≮ BAC = α , se concluye que:
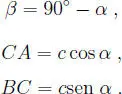
(También está la situación similar AB = c y ≮ ABC = β .)
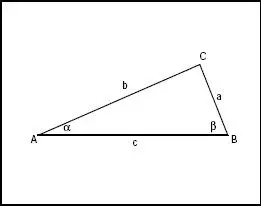
Fig. 1.2
Caso N ◦ 2:Observando la figura 1.2, los datos son el cateto BC = a y el ángulo agudo ≮ ABC = β , luego se obtiene:
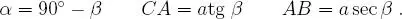
(También está la situación CA = b y ≮ BAC = α .)
Caso N ◦ 3:Observando la figura 1.2, los datos son el cateto BC = a y el ángulo agudo ≮ BAC = α , luego se consigue:
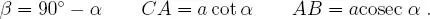
(También está la situación similar CA = b y ≮ ABC = β .)
En lo que viene se utilizarán las notaciones: cos −1= Arccos = INVCOS, sen −1= Arcsen = INVSEN, tg −1= Arctg = INVTAN, que son las simbologías que aparecen en las teclas (o bien como operación secundaria de una tecla) de cualquier calculadora científica para señalar el valor angular asociado a la razón trigonométrica que se presenta cuando se procede a dividir las longitudes de dos lados de un triángulo rectángulo, como también en el sentido notacional matemático actualmente en uso.
Caso N ◦ 4:Observando la figura 1.2, donde los datos son el cateto BC = a y el cateto CA = b , luego se obtiene:
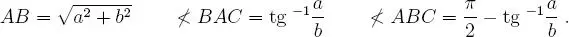
Caso N ◦ 5:Observando la figura 1.2, donde los datos son el cateto BC = a y la hipotenusa AB = c , luego se obtiene:
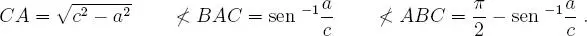
(También está la situación CA = b y AB = c .)
Los casos explicados con anterioridad pueden aplicarse ahora a la resolución de problemas sobre alturas y distancias. Es de suponer que por medio de instrumentos apropiados pueden medirse distancias y ángulos necesarios con una aproximación suficiente para los propósitos que el problema requiere. Es importante tener presente las definiciones de ángulo de elevación y de ángulo de depresión.
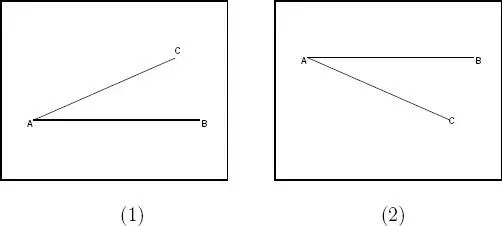
Fig. 1.3
Definición 1.4.1 En la figura 1.3 sea 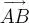 un rayo horizontal en el mismo plano vertical que el objeto C. Se ha trazado también el rayo
un rayo horizontal en el mismo plano vertical que el objeto C. Se ha trazado también el rayo  .
.
(1) En la figura 1.3-(1) donde el objeto C está por encima de la horizontal 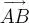 , el ángulo ≮ BAC se llama ángulo de elevación del objeto C visto desde el punto A.
, el ángulo ≮ BAC se llama ángulo de elevación del objeto C visto desde el punto A.
(2) En la figura 1.3-(2) donde el objeto C está por debajo de la horizontal 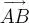 , el ángulo ≮ BAC se llama ángulo de depresión del objeto C visto desde el punto A.
, el ángulo ≮ BAC se llama ángulo de depresión del objeto C visto desde el punto A.
1.5Razones trigonométricas de ángulos compuestos
En las identidades que resumimos en este apartado todos los ángulos que participan, sus sumas, sus diferencias, sus múltiplos y sus submúltiplos serán agudos.
Teorema 1.5.1 Argumento suma.
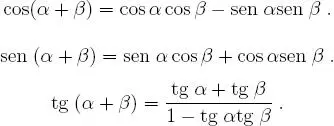
Teorema 1.5.2 Argumento diferencia.
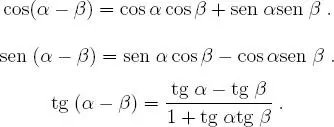
Teorema 1.5.3 Argumento doble.
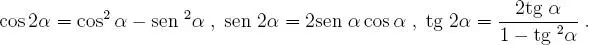
Teorema 1.5.4 Argumento triple.
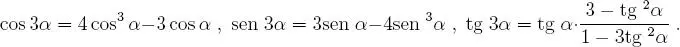
Teorema 1.5.5 Argumento medio.
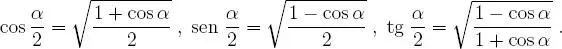
Teorema 1.5.6 Fórmulas de prostaféresis.
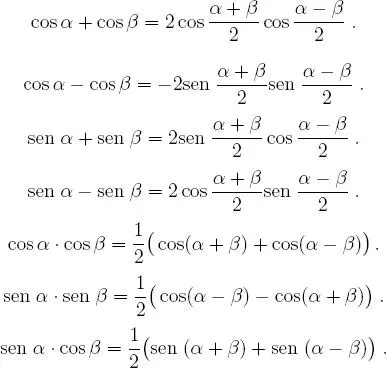 Читать дальше
Читать дальше

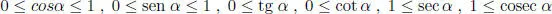

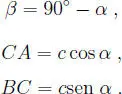

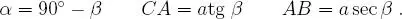
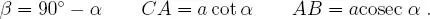
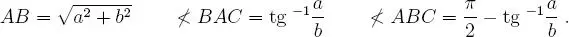
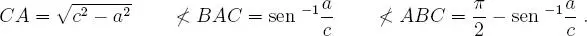

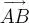 un rayo horizontal en el mismo plano vertical que el objeto C. Se ha trazado también el rayo
un rayo horizontal en el mismo plano vertical que el objeto C. Se ha trazado también el rayo  .
.