“Si hacemos caso de quienes gustan relatar la historia antigua, encontraremos a algunos de ellos refiriendo este teorema de Pythágoras y diciendo que él sacrificó un buey (no habla de hecatombes) en honor de su descubrimiento. Pero, por mi parte, admiro a aquellos que primero observaron la verdad de este teorema (el oriente antiguo) . Y más me maravilla el autor de los Elementos no sólo porque lo valorizó con una lúcida demostración, sino además porque llevó a considerar el teorema aún más general (E.VI.31) por irrefutables argumentos científicos en el libro sexto”.
Por lo demás, es claro que no debemos olvidar los importantes aportes que hicieron en los inicios de la Trigonometría tanto los babilonios, egipcios, griegos, indios y árabes.
Avanzando en la Historia, para resumir, tenemos que en el siglo XV d.C. John Muller, conocido como Regiomontano, escribe un tratado completo de trigonometría, llamado “Tratado del triángulo”. Con posterioridad los astrónomos Tycho Brae, Nicolás Copérnicoy el geómetra Fran¸cois Vi`etedesarrollaron la trigonometría prácticamente hasta el estado actual, aunque a comienzos del siglo XVII Bartolomé Pitiscus, profesor de la Universidad de Heidelberg, escribió el primer texto que llevó el título de “Trigonometría”y la idea del autor era exactamente exponer lo que el nombre implica: medición de triángulos . Faltaría nombrar a Werner, quien encontró las “fórmulas de prostaféresis” , éstas son las identidades conocidas sobre las sumas y diferencias de senos y cosenos.
1.2Razones trigonométricas
En la figura 1.1se considera un determinado ángulo PAQ de medida α -por comodidad no haremos distingo entre ángulo y su medida- y se ha trazado, al arbitrio, la perpendicular 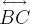 en C al lado
en C al lado 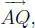 formándose así el triángulo rectángulo ABC . En la definición que sigue deberemos tener presente este triángulo.
formándose así el triángulo rectángulo ABC . En la definición que sigue deberemos tener presente este triángulo.
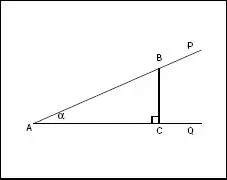
Fig. 1.1
Definición 1.2.1 Tomando en cuenta la figura 1.1 , se llama:
(1)coseno del ángulo α al número:
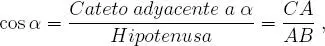
(2)seno del ángulo α al número:
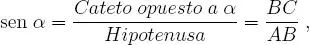
(3)tangente del ángulo α al número:
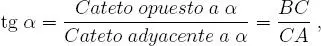
(4)cotangente del ángulo α al número:
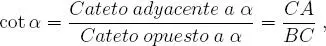
(5)secante del ángulo α al número:
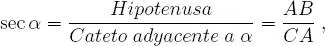
(6)cosecante del ángulo α al número:
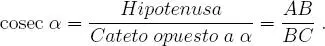
A cada uno de estos números se le denomina razón trigonométrica del ángulo α.
Hacemos notar que estos números llamados razones trigonométricas del ángulo α sólo dependen de α . Esto se debe a que son independientes de la perpendicular  trazada en la figura 1.1(a causa de la semejanza de triángulos rectángulos). O sea, dado un ángulo agudo y positivo α existe uno y sólo un valor para cada razón trigonométrica . En otras palabras, cada razón trigonométrica es una función real con dominio en el intervalo0
trazada en la figura 1.1(a causa de la semejanza de triángulos rectángulos). O sea, dado un ángulo agudo y positivo α existe uno y sólo un valor para cada razón trigonométrica . En otras palabras, cada razón trigonométrica es una función real con dominio en el intervalo0 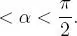 (El lector deberá saber transformar de radianes a grados e inversamente.)
(El lector deberá saber transformar de radianes a grados e inversamente.)
Teorema 1.2.1 Se tienen las siguientes identidades fundamentales:

Como se sabe, el complemento de un ánguloes aquel ángulo que junto con α completan 90 ◦(  radianes), o sea:
radianes), o sea:
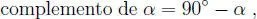
o también:
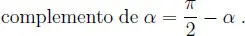
Por esta causa se acostumbra decir que la función cosenoes la cofunción del senoy viceversa; que la cotangentees la cofunción de la tangentey viceversa y, por último, que la cosecantees la cofunción de la secantey viceversa. Es decir:
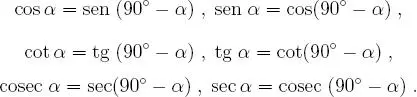
Teorema 1.2.2 Los valores de las razones trigonométricas para los ángulos de 30 ◦ , 45 ◦ y 60 ◦son:

Definición 1.2.2 Los valores de las razones trigonométricas para los ángulos de 0 ◦ , 90 ◦se definen del modo siguiente:

Teorema 1.2.3 Para 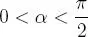 se tiene:
se tiene:
Читать дальше

 en C al lado
en C al lado 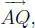 formándose así el triángulo rectángulo ABC . En la definición que sigue deberemos tener presente este triángulo.
formándose así el triángulo rectángulo ABC . En la definición que sigue deberemos tener presente este triángulo.
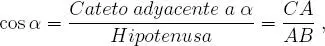
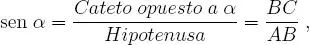
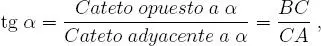
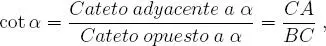
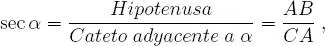
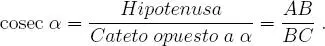
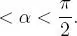 (El lector deberá saber transformar de radianes a grados e inversamente.)
(El lector deberá saber transformar de radianes a grados e inversamente.)
 radianes), o sea:
radianes), o sea: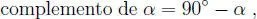
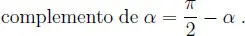
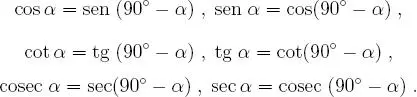


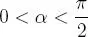 se tiene:
se tiene:










