Gonzalo Masjuán - Trigonometría y geometría analítica

Capítulo 12 Las cónicas

12.1Secciones cónicas

12.2La parábola

12.3La elipse

12.4La hipérbola

12.5Ecuación directriz, foco, excentricidad

12.5.1Dos rectas fijas y las cónicas

12.6La ecuación de segundo grado en dos variables

12.6.1El caso b = 0

12.6.2El caso b ≠ 0

12.6.3El caso σ ≠ 0

12.7Problemas resueltos

12.8Problemas propuestos

12.9Respuestas a los problemas propuestos

Capítulo 13 Superficies

13.1Superficies regladas

13.2Superficie cilíndrica

13.3Superficie cónica

13.4Superficie de revolución

13.5Cuádricas canónicas propias

13.5.1El elipsoide

13.5.2El hiperboloide de un manto

13.5.3El hiperboloide de dos mantos

13.5.4El paraboloide elíptico

13.5.5El paraboloide hiperbólico

13.6La ecuación de segundo grado en tres variables

13.6.1Plano tangente a una cuádrica en un punto de ella

13.6.2Plano polar de un punto con respecto a una cuádrica

13.7Problemas resueltos

13.8Problemas propuestos

13.9Respuestas a los problemas propuestos

Bibliografía

Indice temático

Capítulo 1

TRIGONOMETRIA DEL TRIANGULO RECTANGULO

Según sabemos, el origen de la Trigonometríadebe buscarse en el tiempo en que se hacía el estudio de la esfera celeste, en la cual se suponía que se desplazaban el sol, la luna y las estrellas y cuya posición se calculaba mediante la medición de ángulos. Los dos personajes famosos y más importantes que se interesaron por estos estudios fueron los astrónomos griegos Hiparco de Nicea(siglo II a.C.) y Claudio Ptolomeo(siglo II d.C.). Como consecuencia de lo que hemos mencionado, es fácil creer que la principal, si no única, aplicación de la Trigonometríaes la resolución de triángulos y, por tanto, sus campos de aplicación deberían ser la Astronomía, la Navegación y la Agrimensura. Esto no es así, pues su aplicación en el Cálculo y otras ramas de la Matemática es amplia en nuestros días.

Pues bien, la Trigonometríadesde los inicios, como hemos dicho, se sustenta básicamente en los triángulos rectángulos y, por ende, en el famoso Teorema de Pitágoras. Por tal motivo es pertinente entregar una pequeña biografía de:

Pythágoras, ya que el nombre griego original es Π υθαγo′ραζ (570 a.C. / 480 a.C.). Nació en Samosen fecha muy incierta. No sólo su cronología es dudosa, sino que también lo son casi todos los datos de su vida que nos han entregado todos sus biógrafos principales: Theano (obra perdida), Diógenes Laercio, Jamblico y Porfirio, que se caracterizan por lo visiblemente fantasiosos que son sus relatos en general.

Dejando debida constancia de ello, declaramos que nosotros continuaremos fieles al sano principio metodológico de atenernos a las fuentes existentes, por muy indirectas que sean e inseguras que nos parezcan.

Fue contemporáneo de Thales y, como él, jonio, ya que, como hemos dicho, nació en Samos entre los años 580 a.C. (L olimpíada) y 568 a.C. (LII olimpiada). Su padre era el comerciante Mnesarco, quien traficaba en diversos puntos del extranjero, haciéndose muchas veces acompañar por su hijo.

Hacia 550 a.C. Pythágoras abandona Samos, siguiendo en Lesbos lecciones de filosofía con Ferécides y en Mileto con Thales y Anaximandro. Recorrió luego Fenicia, Arabia, Palestina y Egipto, donde pasó alrededor de veinticinco años en medio de los sacerdotes y sabios de Menfis y Tebas; el colegio sacerdotal de esta última ciudad lo admitió como miembro, iniciándolo en los misterios y cultos de la religión egipcia.

Luego de la conquista de Egipto por Cambises, es llevado a Babilonia, donde estudió la ciencia de los caldeos, hasta que en 512 a.C. obtuvo su libertad y pudo regresar a su patria donde aún vivían sus padres. Visitó enseguida la isla de Creta, Esparta y Delfos, volviendo después a Samos para fundar una escuela que no tuvo acogida.

Disgustado por la opresión del tirano Polícrates, decidió emigrar a Italia, llegando a fundar en Crotona su célebre Escuela Pitagórica. En cierto modo esta Escuela era un instituto filosófico, preocupado de inculcar en sus adeptos no sólo normas morales de vida, sino también determinada concepción del mundo. Platón -y especialmente Aristóteles- se hicieron cargo de analizar y divulgar estos aspectos del llamado “Pitagorismo”. Para nosotros es importante destacar que de todos modos tales concepciones filosóficas y cosmogónicas tenían una evidenciada génesis matemática -se dice que hasta la palabra µαθηµατικη ′: lo que es aprendidohabría sido introducida por Pythágoras- en que los números y las configuraciones geométricas eran ingredientes básicos.

Hacia 509 a.C. se habría casado con una joven llamada Theano, hija, al parecer, de su anfitrión Milón; esa niña habría escrito una biografía del sabio, la cual no ha llegado hasta nosotros.

Pythágoras ejerció una gran influencia sobre sus nuevos conciudadanos, favoreciendo políticamente a la clase aristocrática, motivado tal vez por su formación teocrática en Egipto. Cuando en la ciudad vecina de Sybaris estalló una revolución democrática, los tiranos fueron a refugiarse en Crotona. Pythágoras incitó entonces a los habitantes de ésta contra los sibaritas, los que fueron derrotados e invadidos (510 a.C.). Obtuvo el sabio de ese modo en la ciudad conquistada grandes comodidades para instalar una sección de su Escuela. Sin embargo, hacia 490 a.C. surgió en Crotona un levantamiento popular que llegó a destruir materialmente esa Escuela; su establecimiento en casa de Milón fue incendiado y sus discípulos -muchos de los cuales claudicaron de los principios del maestro en favor de la plebe triunfante- fueron muertos o dispersados.

Pythágoras fue a refugiarse en Tarento, donde languideció y murió oscuramente.

La proposición E.I.47 es conocida en todo el mundo y a través de todas las épocas como el Teorema de Pythágoraspor excelencia. Se cree que este sabio y su Escuela hayan conseguido el enunciado clásico:

“En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa” .

Sin embargo, no hay al respecto una prueba histórica concluyente de tal descubrimiento, tampoco de que el teorema haya sido debidamente demostrado antes de Euclides (el nombre griego original es Eυ’κλEι ′ δηζ ).

El testimonio de DIOGENES LAERCIO (historiador griego que vivió entre los siglos II y III d.C.) en su obra “Vidas, opiniones y sentencias de los filósofos más ilustres, en diez libros”descansa en APOLODORO, apodado el computista, con la consabida inmolación de una hecatombe(cien bueyes) en acción de gracias a los dioses... Nada se nos dice, en cambio, acerca de si los pitagóricos demostraron correctamente el teorema (es posible que hubieran tomado en cuenta la situación presentada en la figura 1).

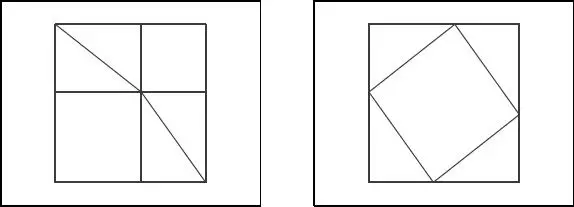
Fig. 1

Bastante más prudente y acertada parece la consideración que de este histórico acontecimiento matemático hace PROCLO (historiador griego que vivió en el siglo V d.C.) en su obra “Comentarios al primer libro de los elementos de Euclides”: