Varios autores - Manual de preparación PSU Matemática
Здесь есть возможность читать онлайн «Varios autores - Manual de preparación PSU Matemática» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Manual de preparación PSU Matemática
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Manual de preparación PSU Matemática: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Manual de preparación PSU Matemática»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
colección de Manuales de preparación PSU elaborada por Editorial Santillana y Ediciones UC tiene como objetivo ser un apoyo eficiente y práctico para el postulante que prepara la Prueba de Selección Universitaria. Cada manual aborda los contenidos de los temarios correspondientes a la respectiva área (Lenguaje y Comunicación, Matemática, Ciencias e Historia, Geografía y Ciencias Sociales) y profundiza en la comprensión y aplicación de las habilidades exigidas por el Marco Curricular vigente. El
Manual de preparación PSU Matemática se ha creado con el objetivo de preparar al estudiante para rendir la PSU correspondiente a esta asignatura. Este material se ha distribuido en virtud de los ejes temáticos considerando los Objetivos Fundamentales (OF) y los Contenidos Mínimos Obligatorios (CMO) que propone el temario DEMRE para la asignatura de Matemática y que han sido definidos en el Marco Curricular.

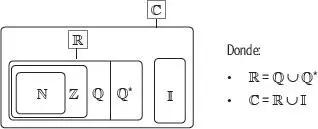
 Los números reales y los números imaginarios son subconjuntos de los números complejos, ya que:
Los números reales y los números imaginarios son subconjuntos de los números complejos, ya que: Igualdad entre números complejos
Igualdad entre números complejos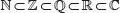 .
.

 o
o 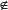 , según corresponda.
, según corresponda.
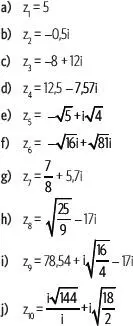
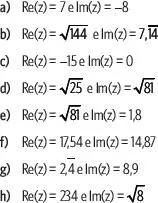
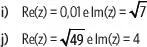
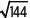 – 7yi, ¿cuáles son los valores de xe ypara que z = w?
– 7yi, ¿cuáles son los valores de xe ypara que z = w?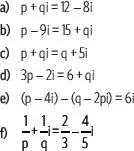
 de un número complejo z = a + bi, como:
de un número complejo z = a + bi, como: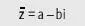
 = a.
= a.