1 ...8 9 10 12 13 14 ...25 4. Ubica en la recta numérica los números –4,2 y  . Luego, intercala un número entre ellos y explica cómo lo hiciste.
. Luego, intercala un número entre ellos y explica cómo lo hiciste.
5. ¿Cuántos números podrías intercalar entre dos números racionales?, ¿por qué?
6. Para cada par de números racionales ubica tres números decimales entre ellos.
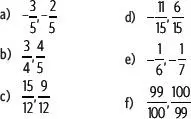
2.4 Operaciones con números decimales
 Adición y sustracción de números decimales finitos
Adición y sustracción de números decimales finitos
Se denomina fracción decimala aquella cuyo denominador es el valor de una potencia entera de 10. Estas fracciones se pueden representar con números decimales finitos.
Para resolver una adicióno una sustracciónentre números decimales finitos se pueden alinear los números por la coma decimal y luego sumarlos como números enteros. Se conserva la ubicación de la coma decimal en el resultado obtenido.
Actividad resuelta
Calcula las siguientes operaciones con números decimales.
a)5,73 + 0,042 + 271,746
Se alinean los sumandos respecto a la coma y se suman como si fueran números enteros.

Por lo tanto, 5,73 + 0,042 + 271,746 = 277,518.
b)15,73 – 18,042
Para calcular la sustracción, se debe calcular la adición 15,73 + (–18,042).
Se restan los valores absolutos y se mantiene el signo del que tiene mayor valor absoluto.

Por lo tanto, 15,73 – 18,042 = –2,312.
 Multiplicación y división de números decimales finitos
Multiplicación y división de números decimales finitos
 Para multiplicar números decimales finitosse resuelve como si fueran números enteros y en seguida se separan tantas cifras decimales en el producto como la suma del número de cifras decimales de los factores.
Para multiplicar números decimales finitosse resuelve como si fueran números enteros y en seguida se separan tantas cifras decimales en el producto como la suma del número de cifras decimales de los factores.
 Para dividir números decimales finitosse pueden amplificar los términos de la división por el valor de una potencia de 10, de modo que el divisor sea un número entero.
Para dividir números decimales finitosse pueden amplificar los términos de la división por el valor de una potencia de 10, de modo que el divisor sea un número entero.
 Cuando los números decimales son infinitos periódicoso semiperiódicos, estos se pueden escribir en su forma fraccionaria y luego resolver las operaciones que correspondan.
Cuando los números decimales son infinitos periódicoso semiperiódicos, estos se pueden escribir en su forma fraccionaria y luego resolver las operaciones que correspondan.
Actividad resuelta
Calcula las siguientes operaciones con números decimales.
a)2,75 • 0,73

b)2,304 : 0,0096

Actividades
1. Resuelve las siguientes adiciones.
a)0,030 + 0,5
b)0,075 + 0,25
c)0,83 + 0,27
d)0,45 + 0,187
2. Escribe los números decimales del ejercicio anterior en su forma fraccionaria y resuelve las adiciones correspondientes. Compara los resultados obtenidos.
3. Resuelve las siguientes sustracciones.
a)0,030 – 0,5
b)0,075 – 0,25
c)0,83 – 0,27
d)0,45 – 0,187
4. Escribe los números decimales del ejercicio anterior en su forma fraccionaria y resuelve las sustracciones correspondientes. Compara los resultados obtenidos.
5. Resuelve las siguientes multiplicaciones.
a)7,34 • 0,89
b)2,03 • 0,009
c)3,75 • 4,01
d)5,371 • 1,46
6. Resuelve las siguientes divisiones.
a)0,0017 : 0,034
b)5,832 : 7,2
c)0,1331 : 1,21
d)47,239 : 0,0001
7. Resuelve las siguientes adiciones y sustracciones de números decimales.
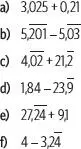
8. Escribe los números decimales del ítem 7 en su forma fraccionaria y realiza las operaciones correspondientes. Luego, compara los resultados.
9. Lee la siguiente información y luego responde.
Una ampolleta se calienta cuando la electricidad pasa a través del filamento. La cantidad de energía eléctrica transformada en energía calórica por el flujo de corriente está dada por la fórmula:
w = R • I 2• t
donde wes la energía calórica medida en joules (J), Res la resistencia del filamento en ohms, Ies la corriente en amperes (A) y tes el tiempo en segundos.
a)Calcula el valor de la resistencia de un filamento si la energía calórica obtenida por una corriente eléctrica de 12,456 A durante 15 segundos es 83.771,8097 J.
b)Realiza el cálculo anterior con una calculadora. ¿Obtuviste el mismo resultado?, ¿por qué?
c)¿Qué aproximación realiza tu calculadora, por redondeo o por truncamiento? Justifica tu respuesta.
3. Números reales ( 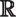 )
)
3.1 El conjunto de los números reales
 Números irracionales (
Números irracionales ( 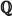 * )
* )
El conjunto de los números irracionalesse simboliza como  * y está formado por todos los números que no se pueden escribir de la forma
* y está formado por todos los números que no se pueden escribir de la forma 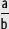 , con a, b ∈
, con a, b ∈  , b ≠ 0. Por lo tanto, su forma decimal tiene infinitas cifras decimales noperiódicas.
, b ≠ 0. Por lo tanto, su forma decimal tiene infinitas cifras decimales noperiódicas.
Читать дальше

 . Luego, intercala un número entre ellos y explica cómo lo hiciste.
. Luego, intercala un número entre ellos y explica cómo lo hiciste.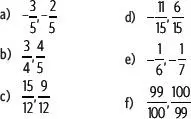
 Adición y sustracción de números decimales finitos
Adición y sustracción de números decimales finitos

 Para multiplicar números decimales finitosse resuelve como si fueran números enteros y en seguida se separan tantas cifras decimales en el producto como la suma del número de cifras decimales de los factores.
Para multiplicar números decimales finitosse resuelve como si fueran números enteros y en seguida se separan tantas cifras decimales en el producto como la suma del número de cifras decimales de los factores.

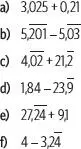
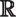 )
)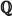 * )
* ) * y está formado por todos los números que no se pueden escribir de la forma
* y está formado por todos los números que no se pueden escribir de la forma 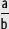 , con a, b ∈
, con a, b ∈  , b ≠ 0. Por lo tanto, su forma decimal tiene infinitas cifras decimales noperiódicas.
, b ≠ 0. Por lo tanto, su forma decimal tiene infinitas cifras decimales noperiódicas.










