Asdrúbal Valencia Giraldo - Ciencia de los metales

Como se muestra en la figura 7.24, solo se requiere un esfuerzo aplicado relativamente pequeño para mover la dislocación en el plano de deslizamiento. Este se puede entender así: en una red perfecta, todos los átomos por encima y por debajo del plano de deslizamiento están en sus posiciones de mínima energía; cuando los átomos se desplazan, sobre todos ellos actúa la misma fuerza opuesta al movimiento. Cuando hay una dislocación en la red de átomos lejanos a la dislocación, todavía están en sus posiciones de mínima energía, pero los que se hallan en la dislocación, no lo están. Los átomos próximos a la dislocación se encuentran colocados de manera simétrica a los lados opuestos del semiplano extra y ejercen fuerzas iguales y opuestas sobre los átomos de la dislocación. En esta descripción, tan simplificada, no hay fuerza neta sobre la dislocación y el esfuerzo necesario para moverla es cero.

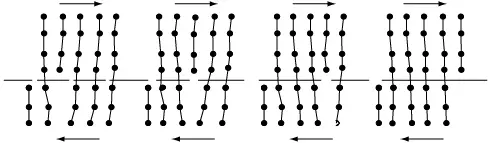
Figura 7.24 Movimiento de una dislocación de borde

Sin embargo, en la práctica, ciertas condiciones de simetría dan origen a una resistencia de la red al movimiento de las dislocaciones, llamada fuerza de Peierls-Nabarro, pero que es mucho menor que el esfuerzo cizallante teórico.

7.5.1. La fuerza de Peierls-Nabarro

Lo discutido en el último párrafo es válido cuando las dislocaciones ocurren en una situación simétrica, pero no en el momento en que pasan por situaciones asimétricas; en este caso se requiere una fuerza para mover la dislocación, la de Peierls-Nabarro.

Una característica importante de esta fuerza es que su magnitud varía periódicamente a medida que la dislocación se mueve a través de la red.

Se sabe que la magnitud de la fuerza de Peierls-Nabarro depende en gran parte del ancho (w) de la dislocación (que representa la distancia sobre la cual se distorsiona la red debido a la dislocación) (véase figura 7.25) y de la distancia entre planos similares (d0).

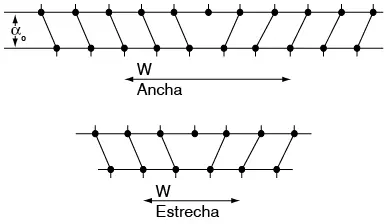
Figura 7.25 Amplitud característica de una dislocación de borde, la cual afecta la fuerza de Peierls-Nabarro

La expresión más simple para la tensión de Peierls-Nabarro se basa en la ecuación 7.3. La expresión aproximada es:

τp-n = e(–2πw) ⁄ b) (7.5)

y

w = d0/(1 – γ).

Según la ecuación 7.5, la tensión de Peierls para un plano dado disminuye con d0. Como la distancia entre planos varía inversamente con la densidad atómica de estos, el deslizamiento es más fácil en los planos con empaquetamiento atómico más denso. Además, la tensión de Peierls depende de w, que es función de la estructura atómica y el tipo de enlace. En las estructuras densas (fcc y hcp), w es grande y, por tanto, τp–n es bajo. En los cristales covalentes iónicos bcc ocurre lo contrario.

Puesto que τp–n depende de lo que suceda en el núcleo de la dislocación, es sensible a la energía térmica de la red y, por tanto, está condicionado a la temperatura. A bajas temperaturas, donde el incremento térmico del movimiento de las dislocaciones es limitado, la tensión de Peierls es elevada. Debe tenerse en cuenta, además, que la resistencia de la red al movimiento de las dislocaciones está condicionada no solamente por la tensión de Peierls, sino también por la orientación de la línea de dislocación dentro de la red cristalina.

Después de esta corta anotación sobre la tensión de Peierls, y volviendo al tema en sí del movimiento de la dislocación, en la figura 7.26 se ve que el movimiento de una dislocación a través del plano de deslizamiento hasta la superficie del metal produce un peldaño igual al vector de Burgers de la dislocación. La dirección de deslizamiento es siempre necesariamente paralela al vector de Burgers de la dislocación causante del deslizamiento.

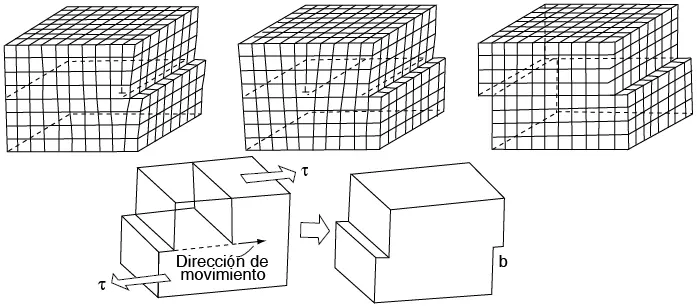
Figura 7.26 Creación de un peldaño de deslizamiento por movimiento de una dislocación de borde, a. de derecha a izquierda; b. de izquierda a derecha.

En la figura 7.26, la dislocación de borde se ha movido en el plano de deslizamiento, definido unívocamente por la posición de la línea de dislocación y su vector de Burgers; por consiguiente, el movimiento conservativo de una dislocación de borde está limitado a un plano específico. Por otro lado, en la figura 7.27 se puede ver el movimiento de una dislocación de tornillo pura y también visualizar como si ocurriera en un plano de deslizamiento, el LMNO, y la formación de un peldaño de deslizamiento (véase figura 7.28), similar al de la figura 7.26.

Sin embargo, la línea de la dislocación de tornillo y su vector de Burgers no definen un plano único y el movimiento de la dislocación no está restringido a un plano específico. Se notará que el desplazamiento de los átomos y, por tanto, del peldaño de la dislocación de tornillo son paralelos a la línea de dislocación. Esto se puede apreciar mejor si se considera una vista en planta de los átomos situados por encima y por debajo del plano que contiene la dislocación (véase figura 7.29).

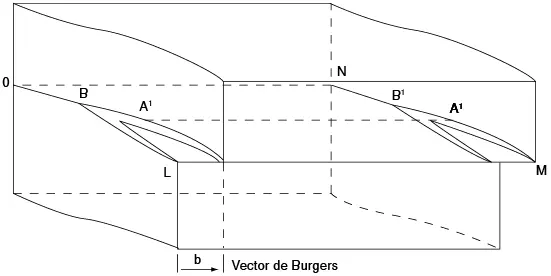
Figura 7.27 Formación y movimiento de una dislocación de tornillo pura desde AA’ hasta BB’

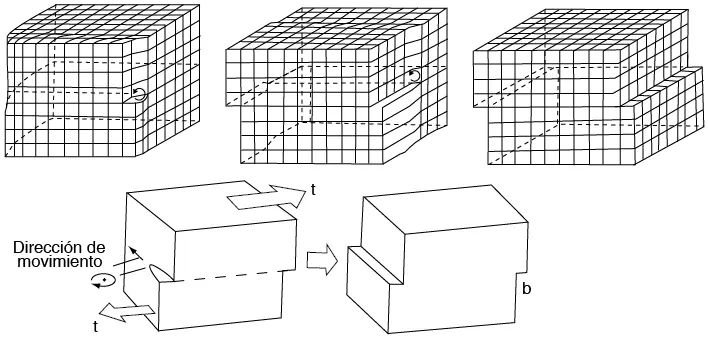
Figura 7.28 Creación de un peldaño de deslizamiento por el movimiento de una dislocación de tornillo

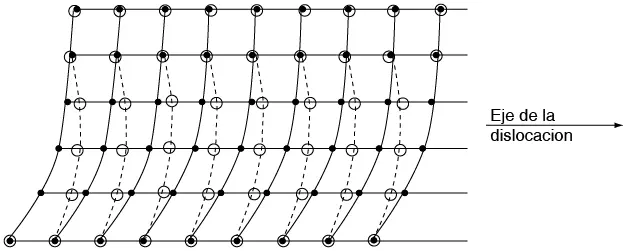
Figura 7.29 Colocación de los átomos alrededor de una dislocación de tornillo

El movimiento de la dislocación de tornillo produce un desplazamiento paralelo a la línea de dislocación, es decir, puede pasar de un plano de deslizamiento a otro adyacente, siempre que posean una dirección común de deslizamiento.

7.5.2. Deslizamiento cruzado

Como las dislocaciones de tornillo son libres de vagar por fuera de sus planos originales de movimiento, pueden tomar parte en el deslizamiento cruzado y en reacciones complicadas con otras dislocaciones, lo cual lleva a la formación de redes complejas de dislocación. El deslizamiento cruzado se puede visualizar con ayuda de la figura 7.30.

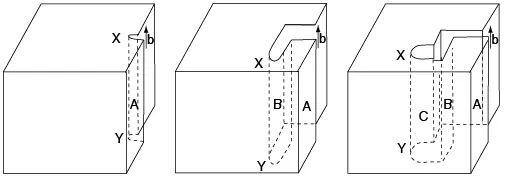
Figura 7.30 Deslizamiento cruzado de la dislocación de tornillo XY del plano A al B y de nuevo al A

El deslizamiento siempre ocurre en dirección del vector de Burgers b.

Al principio de la deformación plástica, la dislocación de tornillo XY se mueve sobre el plano A. Si la continuación del movimiento en el plano A se ve impedida por un obstáculo, como una partícula, la dislocación de tornillo puede cruzar sobre otro plano equivalente, como B, y continuar su movimiento (véase figura 7.30). Como el vector de Burgers no cambia, el deslizamiento continúa en la misma dirección, aunque en un plano diferente. La dislocación de tornillo puede continuar sobre el plano B o regresar al plano A por un segundo proceso de deslizamiento.