Asdrúbal Valencia Giraldo - Ciencia de los metales

Para que este concepto sea válido es necesario que: 1) el movimiento de una dislocación a través del cristal requiera un esfuerzo mucho menor que el teórico (esto ya fue discutido en la sección 7.4); y 2) el movimiento de la dislocación produzca un peldaño o banda de deslizamiento en la superficie libre (esto fue discutido en la sección 7.4 y esquematizado en las figuras 7.35 a 7.38). Por eso, la deformación plástica de los metales se explicó perfectamente por el movimiento de las dislocaciones, aun antes de lograr evidencia experimental como la que se posee en la actualidad.

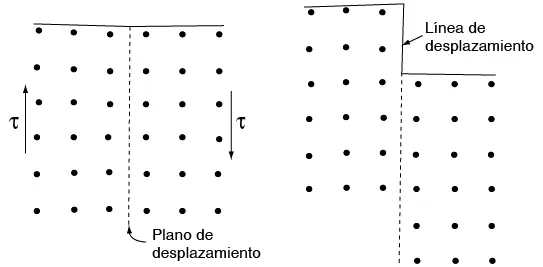
Figura 7.42 Idea clásica del deslizamiento

7.6.3. Tensión cizallante crítica resuelta

La magnitud del deslizamiento en un monocristal depende de la tensión cizallante producida por las cargas externas, la geometría de la estructura del cristal y la orientación de los planos de deslizamiento activos con respecto a las tensiones cizallantes (véase figura 7.43).

Si de un metal dado se toman cristales con diferentes orientaciones y se deforman en tracción, las curvas σ-ε muestran grandes variaciones. La tensión de cedencia, la resistencia última y el alargamiento son todos marcadamente anisotrópicos, aun en los cristales cúbicos. Por ejemplo, la tensión de fluencia de los cristales de Zn varía en un factor de 6 cuando se cambia de orientación. Así, para poder comparar el comportamiento de cristales con diferentes orientaciones, es costumbre resolver la tensión de tracción en su componente en la dirección de deslizamiento y sobre el plano de deslizamiento.

En la figura 7.43, un cristal de área seccional A tiene una carga de tracción F aplicada de modo que origina una tensión de tracción σ. El plano de deslizamiento se muestra con su dirección de deslizamiento OX y λ es el ángulo entre el eje de carga y la dirección de deslizamiento. El eje hace un ángulo χ con el plano, de modo que el área del plano es

A′ = A/senχ.

Por consiguiente, la tensión de tracción sobre el plano es:

(F/A)senχ = σsenχ

y la tensión cizallante en el plano, resuelta en la dirección de deslizamiento, es:

τ = σ senχcosλ = σ cos ϕcosλ, (7.6)

donde M = σcosϕcosλ se denomina factor de Schmid y ϕ es el ángulo entre el eje y la normal ON al plano.

Si el esfuerzo es normal al plano, λ = 90° y τ = 0. Si el eje de tracción es paralelo al plano, χ = 0 y τ = 0. En estos dos extremos no hay deformación por deslizamiento, pues τ = 0.

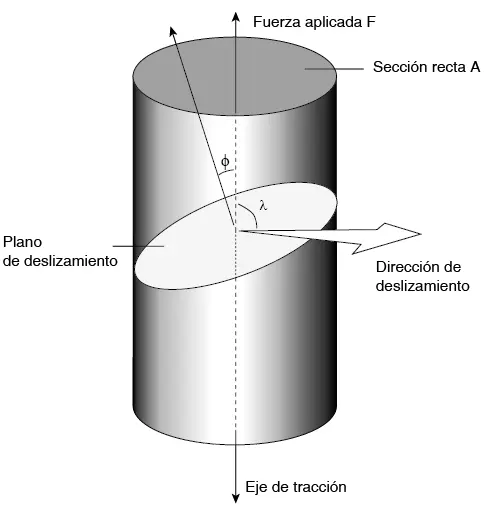
Figura 7.43 Tensión cizallante resuelta sobre el sistema de deslizamiento

Aunque la fluencia varíe con la orientación, si el esfuerzo de fluencia se convierte en una tensión cizallante resuelta mediante la ecuación 7.6, se encuentra que la tensión cizallante crítica resuelta τ0 sobre el plano de deslizamiento es una constante para un metal dado. En otras palabras, el deslizamiento sobre el plano y en la dirección de deslizamiento alcanza un umbral τ0 llamado tensión cizallante crítica resuelta. Este valor es, en el monocristal, equivalente al esfuerzo de cedencia en una curva tensión-deformación corriente y depende de la composición y la temperatura. Esta condición se denomina ley de Schmid.

En la figura 7.44 se muestra la curva teórica para la ecuación 7.7:

τ0 = σ0senχ0cosλ0, (7.7)

donde:

τ0 = tensión cizallante crítica resuelta.

σ0 = tensión fluencia en tracción.

λ0 = ángulo inicial entre la dirección de deslizamiento y el eje de tracción.

χ0 = ángulo inicial entre el plano de deslizamiento y el eje de tracción.

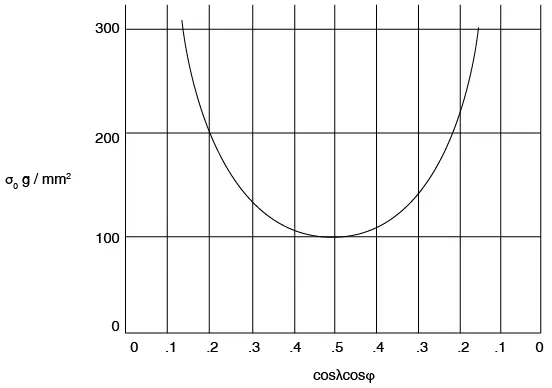
Figura 7.44 Tensión de fluencia en función de la orientación, en monocristales de Mg

La ley de Schmid se ha comprobado experimentalmente, sobre todo en metales hexagonales (véase figura 7.44). En la figura 7.45 se muestran los resultados experimentales, comparados con los predichos por la ley de Schmid para Zn de alta pureza. La hipérbola se obtiene suponiendo un τ0 = 180 kPa.

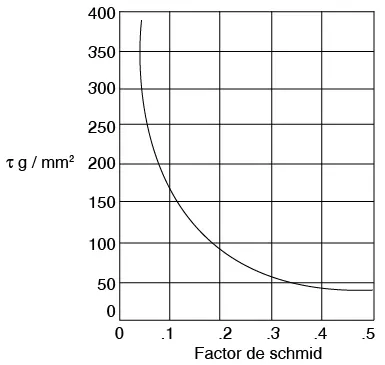
Figura 7.45 Variación de la tensión de fluencia con la orientación, en monocristales de Zn

Para los cristales cúbicos, la correspondencia entre los resultados experimentales y la ley de Schmid no es tan buena. Esto se debe principalmente al número elevado de sistemas de deslizamiento que pueden operar de manera simultánea. Sin embargo, τ0 representa una propiedad mecánica fundamental, por su estrecha relación con el modo básico de deformación plástica por cizallamiento sobre los planos de deslizamiento.

La tensión cizallante crítica resuelta es muy sensible a la estructura, sobre todo a la composición, la temperatura y la tasa de deformación. En la figura 7.46 se muestra la variación de τ0 con la temperatura para varios cristales. Nótese que la diferencia en magnitud aumenta a bajas temperaturas; esta variación se debe a que τ0 está determinado por la interacción entre las dislocaciones y otros defectos, como las vacancias e impurezas, todo lo cual es dependiente de la temperatura.

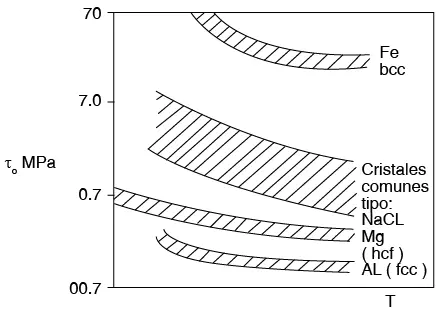
Figura 7.46 Variación de τ0 con la temperatura (T), para varios tipos de materiales

La tensión cizallante crítica resuelta es, por supuesto, mayor que el esfuerzo necesario para mover una dislocación, pero mucho menor que el teórico que se requiere para producir deslizamiento en una red perfecta. Según lo anterior, τ0 debe decrecer al disminuir la densidad de defectos; esto indicaría que los cristales de alta pureza fluirían con tensión cero sin exhibir comportamiento elástico. Sin embargo, el trabajo con metales de la más elevada pureza muestra que siempre hay un límite elástico, aunque este ocurre a niveles de tensión extremadamente bajos.

7.6.4. Deformación por maclas

Después del deslizamiento de dislocaciones, el maclado es el mecanismo más importante de deformación plástica, aunque no es tan común como aquel. La diferencia más obvia entre un cristal deslizado y uno maclado es el cambio de forma resultante en cada caso. La deformación por maclado fue descubierta en los cristales naturales (véase figura 7.47). Mientras el deslizamiento comprende una translación simple sobre un plano de deslizamiento de modo tal que una porción rígida del sólido se mueva con relación a la otra, el cuerpo maclado sufre un cambio de forma (véase figura 7.48).

Figura 7.47 Deformación por maclado. Las maclas fueron descubiertas en los cristales de los minerales naturales

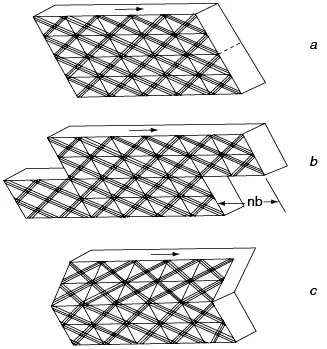
Figura 7.48 Cambio de forma en un cristal