a. Sin deformar; b. deslizado nb; c. maclado, revelando la reorientación en la macla.
La zona deformada por maclado es una región de un cuerpo cristalino que ha sufrido una deformación homogénea, de tal manera que la estructura resultante es idéntica a la original, pero con diferente orientación. El movimiento de dislocaciones asociado con el deslizamiento se presenta en múltiplos del vector de Burgers (nb) (véase figura 7.48b). En contraste, el sólido maclado resulta de los movimientos en la macla sobre todos los planos y en cantidades fraccionales. Como se ve en la figura 7.48c, el desplazamiento en un plano de la macla es proporcional a su distancia al límite macla-matriz.
Si se examinan más de cerca estos desplazamientos de macla en un cristal cúbico, se ve que el proceso de maclado ha efectuado una rotación de la red tal que las posiciones de los átomos en la macla representan una imagen especular de los que están en la región sin maclar (véase figura 7.49).

Figura 7.49 Macla en el plano (120) en un cristal cúbico simple
Por otro lado, el deslizamiento ocurre con translaciones sobre planos espaciados en múltiplos del vector de Burgers, de modo que la orientación relativa de las diferentes regiones permanece inalterada.
El maclado no es el modo dominante de deformación en los metales que poseen muchos sistemas de deslizamiento, por ejemplo los fcc, aunque es muy significativo en metales donde los sistemas sean limitados, como los hcp, donde el deslizamiento está limitado al plano basal. Un monocristal de Zn se deforma fácilmente por deslizamiento basal si el plano está adecuadamente orientado; pero si, por ejemplo, el plano basal es paralelo al eje de tracción, el cristal se deformará por maclado.
El mecanismo de maclado también se da en metales fcc a baja temperatura.
La mejor manera de apreciar la transformación que se da en el maclado es considerar un monocristal esférico (véase figura 7.50), en el cual el plano de macla K1 se muestra como un plano ecuatorial y η1 es la dirección de la cizalladura.
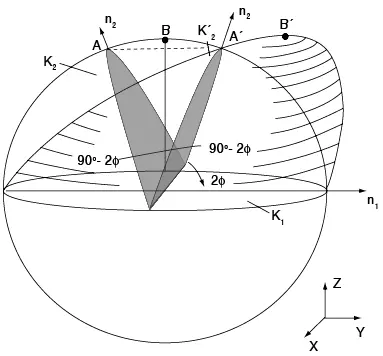
Figura 7.50 Geometría del maclado
También se necesita conocer la magnitud de la cizalladura S, que se define como la distancia que se mueve un punto situado a una longitud unitaria del plano de macla. Si el hemisferio superior se macla, se distorsiona como un elipsoide (véase figura 7.50), en el cual solamente dos planos permanecen sin distorsionar, es decir, todavía son de forma semicircular, el plano de macla K1 y otro plano K2 que está sombreado en el diagrama. El plano de cizallamiento se define como el plano que contiene la dirección η1 y la normal al plano de macla K1; a su vez, la intersección del plano de cizallamiento con el segundo plano, sin distorsionar K2, se identifica como η2.
Un criterio más de la transformación por maclado es que el segundo plano no distorsionado K2 tiene el mismo ángulo con K1 antes y después de la transformación.
Si se supone que la esfera tiene radio unitario, la magnitud del cizallamiento S está representada por la distancia BB’, que se puede expresar en términos del ángulo ٢ϕ entre los planos no distorsionados:
S = 2cotϕ. (7.6.3)
Por consiguiente, si se encuentran los dos planos sin distorsionar, la deformación cizallante en la macla se determina midiendo el ángulo interplanar. En la tabla 7.4 se dan valores típicos.
Tabla 7.4 Algunos datos cristalográficos de maclas
| Metal |
Estructura del cristal |
Índices de macla |
Cizallamiento |
| K1 |
η1 |
K2 |
η2 |
| Cu y otros fcc |
fcc |
111 |
112 |
111 |
112 |
0,707 |
| Fe-a |
bcc |
112 |
111 |
112 |
111 |
0,707 |
| Mg |
hcp, c/a = 1,624 |
1012 |
1011 |
1011 |
1011 |
0,129 |
| Zn |
hcp, c/a = 1,856 |
1012 |
1011 |
1011 |
1011 |
0,139 |
| Cd |
hcp, c/a = 1,866 |
1012 |
1011 |
1011 |
1011 |
0,171 |
| Sn-b |
Tetragonal |
301 |
103 |
101 |
101 |
0,119 |
| Bi |
Romboédrico |
110 |
001 |
001 |
110 |
0,118 |
La transformación por maclado, que lleva a un cambio en la orientación de la región maclada, no altera la simetría o estructura del cristal, algo demostrado por la difracción de rayos X. Por consiguiente, el tamaño y la forma de la celda no se ven alterados por la transformación, y como resultado de ello debe haber tres vectores de la red (no coplanares) que tienen las mismas magnitudes y relaciones angulares antes y después del maclado. Como K1 y K2 son los únicos planos no distorsionados, los tres vectores deben residir en esos dos planos.
Si ahora se considera cualquier vector ε en el plano K1 (véase figura 7.51), se deduce que η2 es el único vector del plano K2 que hace el mismo ángulo θ con ε antes y después del maclado. Esto es así porque η2 es el único vector perpendicular a la intersección de dos planos K1 y K2. Esta condición se aplica a ε y a cualquier otro vector que está en K1. Si se supone que K1 es un plano racional que contiene direcciones racionales y que η2 es racional, se tiene el requerimiento de tres vectores no coplanares que no cambian de magnitud ni de relación angular durante el maclado.
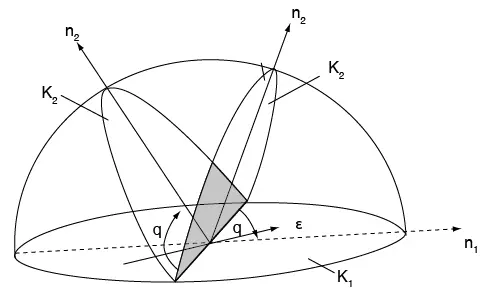
Figura 7.51 Los vectores constantes del maclado
Del mismo modo se puede demostrar que η1, que es perpendicular a la intersección de K1 y K2, es el único vector que hace el mismo ángulo con vectores arbitrarios en K2 antes y después del maclado. Así que los requerimientos del maclado también se reúnen si la dirección η1 y el plano K2 son racionales.
Hay una tercera posibilidad y es que ambos planos K1 y K2 y los dos vectores η1 y η2 sean todos racionales.
En resumen, hay tres tipos o modos de cizallamiento que preservan la simetría de la estructura del metal y satisfacen las condiciones del maclado:
1 Maclas de primera clase: plano K1 racional, dirección η2 racional.
2 Maclas de segunda clase: plano K2 racional, dirección η2 racional.
3 Maclas racionales o compuestas: K1 y K2 racionales, η1 y η2 racionales.
Así que la naturaleza exacta de la rotación de la red durante el maclado dependerá del tipo de macla que ocurra. La mayoría de los metales caen dentro de la tercera clase, debido a sus estructuras de alta simetría.
Para definir completamente un proceso de maclado debe especificarse los índices de los planos K1 y K2 y las direcciones η1 y η2, junto con el cizallamiento S. En la tabla 7.4 se dan datos típicos para algunos metales.
La tensión necesaria para producir maclas es, en general, mayor y menos sensible a la temperatura que la que se requiere para el deslizamiento. Esta tensión, para iniciar, es mucho mayor que la tensión indispensable para propagarla.
Las maclas se pueden generar por deformación mecánica o como resultado del recocido después de la deformación plástica. Las del primer tipo se conocen como maclas mecánicas y las otras como maclas de recocido. Las maclas mecánicas se producen en metales bcc o hcp, bajo condiciones de carga rápida y bajas temperaturas.
Читать дальше