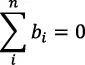Asdrúbal Valencia Giraldo - Ciencia de los metales

Figura 7.15 Frederick Charles Frank (1911-1998). Propuso el circuito de Burgers.

Fuente: Your.org (s. f.).

Téngase en cuenta que si el procedimiento se sigue al contrario, es decir, como se ilustra en la figura 7.17, el vector SF es el vector local de Burgers. En general, el vector local es diferente al vector verdadero.

Algo que se observa de la definición del vector de Burgers es que en una dislocación de borde, el vector b forma un ángulo recto con la línea de dislocación t.

Cuando el circuito se hace alrededor de una dislocación de hélice (véase figura 7.18), el vector de Burgers es paralelo a la línea de dislocación t.

Aunque parezca redundante, es bueno escribir de nuevo estas dos reglas:

1 El vector de Burgers de una dislocación de borde es normal a la línea de dislocación.

2 El vector de Burgers de una dislocación de tornillo es paralelo a la línea de dislocación.

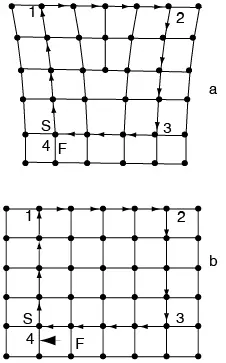
Figura 7.16 Circuito de Burgers en: a. un cristal real y b. un cristal perfecto

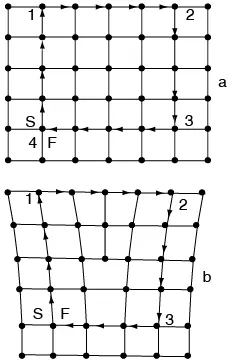
Figura 7.17 Circuito SF en un cristal perfecto y en uno real

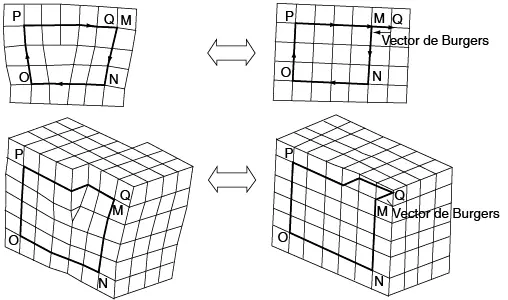
Figura 7.18 Circuito y vector de Burgers en una dislocación de hélice

En el caso general de una dislocación mixta, la línea de dislocación forma un ángulo arbitrario con su vector de Burgers. Sin embargo, el vector de Burgers de la dislocación es siempre el mismo e independiente de la posición de la dislocación (véase figura 7.19). Si el vector cambia, la dislocación ya no será idéntica a sí misma.

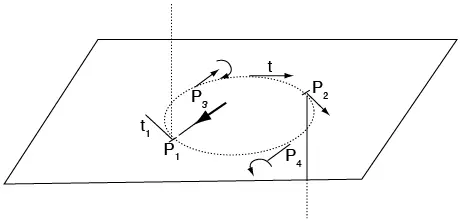
Figura 7.19 El vector de Burgers es siempre el mismo. En P1 y P2, la dislocación es de borde (pues

b ┴ t1) y en P3 y P4 la dislocación es de tornillo (pues b es paralelo a la línea de dislocación). En otros puntos es mixta.

7.4. Anillos de dislocaciones

En los cristales reales, las dislocaciones son curvas en la mayoría de los casos, como se ve en la figura 7.20. Es decir, tienen componentes de borde y tornillo. A pesar de que el vector de Burgers, b, es el mismo en toda la dislocación, se ve que la dislocación es de tornillo en A y de borde en B. El lector puede comprobarlo trazando los circuitos de Burgers correspondientes alrededor de A y B. En todos los puntos entre A y B, la dislocación tiene componentes de borde y de tornillo, es una dislocación mixta.

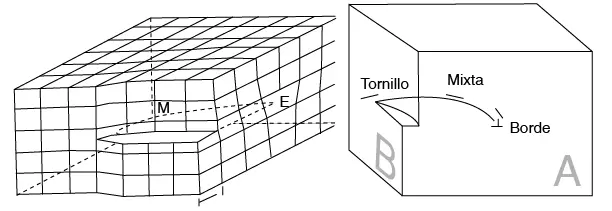
Figura 7.20 Dislocación curva con componentes de borde y tornillo

Por su naturaleza, las dislocaciones no pueden terminar dentro, sino que deben extenderse hasta una superficie exterior del cristal. Sin embargo, en vez de una línea extendida, puede formar un anillo (se dice “anillo” significando cualquier trayectoria cerrada).

En la figura 7.21a se indica un anillo de dislocaciones de forma cuadrada. En el cristal se hacen los cortes AAAA y BBBB. Las figuras 7.21b y c muestran esas secciones y se puede visualizar que los segmentos CF y DE del anillo, representados en la figura 7.21b, son dislocaciones de borde, mientras que los segmentos CD y FE (véase figura 7.21c) son de tornillo, de acuerdo con la dirección de cizallamiento mostrada.

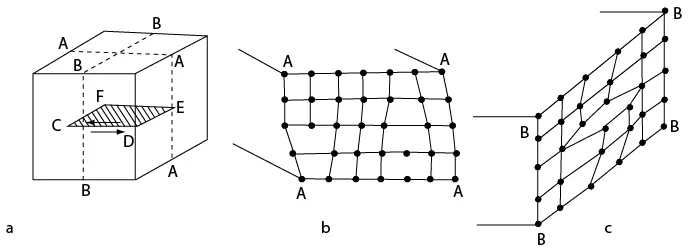
Figura 7.21 Circuito (anillo) cuadrado de dislocación. a. anillo de dislocaciones de forma cuadrada. b y c, secciones AAAA y BBBB respectivamente.

Un anillo puede visualizarse como un corte hecho en un cristal seguido de un cizallamiento. Las dislocaciones CF y DE (lo mismo que la CD y FE) son del mismo tipo, pero de signo opuesto.

En resumen, una línea de dislocación no puede terminar dentro de una región del cristal que de otro modo sería perfecta, sino que debe hacerlo en una superficie libre, que puede ser una intercara, otra dislocación o algún otro defecto. Esto incluso se ha demostrado desde el punto de vista formal del continuo elástico. Por consiguiente, las dislocaciones generan anillos o redes con ramificaciones que terminan en la superficie (véase figura 7.22).

Cuando tres o más dislocaciones se unen en un punto o nodo, es condición necesaria que la suma de los vectores de Burgers sea igual a cero. Considérese la dislocación b1 (véase figura 7.23), que se ramifica en dos dislocaciones de vectores de Burgers b2 y b3. Se ha trazado un circuito de Burgers alrededor de cada dislocación y en el mismo sentido. Del diagrama se ve que:

b1 = b2 + b3.

Esto es válido cuando las dislocaciones son del mismo sentido, es decir, cuando las dislocaciones se combinan para formar una tercera, o cuando se disocia en dos. Si se cambia la dirección de b1 quedaría:

b1 + b2 + b3 = 0.

Esta forma es más común y permite escribirla más fácilmente si se tiene que el sentido de los vectores es positivo cuando apuntan hacia afuera del nodo.

En general:

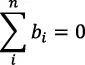
Cuando n dislocaciones se reúnen en un nodo, lo cual es análogo a la ley de Kirchoff en electricidad, los vectores de Burgers se conservan.

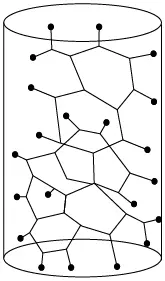
Figura 7.22 Diagrama que ilustra la red de dislocaciones en un cristal. Las dislocaciones pueden terminar solamente en un anillo, en un nodo, en un defecto o en una superficie.

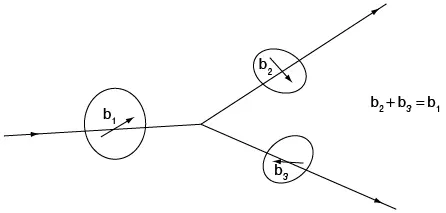
Figura 7.23 Tres dislocaciones que forman un nodo

7.5. Movimiento de dislocaciones

Hay dos tipos básicos de movimiento de dislocaciones: el deslizamiento o movimiento conservativo, en el cual las dislocaciones se mueven en una superficie que contiene tanto la línea de dislocación t como su vector de Burgers b, y el movimiento no conservativo, en el que las dislocaciones se mueven fuera de la superficie de deslizamiento. Esto, considerando las dislocaciones desde el punto de vista elemental. En la realidad, y principalmente para deformaciones plásticas elevadas, existen interacciones complejas entre las dislocaciones. Sin embargo, estas interacciones son el resultado de los mecanismos básicos mencionados, que son los que se estudian aquí.

En la sección 7.1 se mostró que el esfuerzo cizallante teórico necesario para el deslizamiento era muchas veces mayor que el observado experimentalmente, τc. Este bajo valor se debe al movimiento de las dislocaciones.