Asdrúbal Valencia Giraldo - Ciencia de los metales

Con la introducción de un semiplano extra de átomos en la red, como se ve en la figura 7.7, los mencionados autores pudieron demostrar que la rotura de enlaces en el plano de deslizamiento se puede restringir a la vecindad inmediata del extremo inferior del semiplano extra (llamado línea de dislocación). A medida que la línea de dislocación se mueve a través del cristal (como el pliegue en una alfombra o como el avance de una oruga), la rotura de los enlaces se da de manera consecutiva y no simultáneamente, como era necesario en la red perfecta (véase figura 7.1).

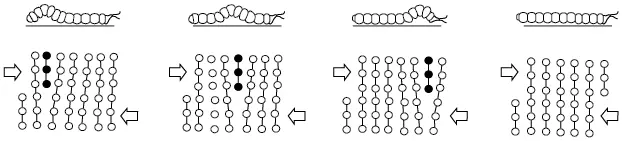
Figura 7.7 Defecto de la red causado por la introducción de un semiplano extra de átomos

Obsérvese como el semiplano extra se mueve a través de la red cristalina semejante al movimiento que hace una oruga al desplazarse.

Figura 7.8 Johannes Martinus Burgers (1895-1981). Teórico de la dislocación de tornillo.

Fuente: Wikipedia (s. f. 5).

Este tipo de dislocación propuesto por Polanyi, Orowan y Taylor vino a ser conocido como dislocación de cuña o de borde. Este concepto permaneció sin mucho desarrollo hasta después de la Segunda Guerra Mundial, a pesar de que en 1939 Johannes Martinus Burgers (véase figura 7.8) conceptualizó otro tipo de dislocación que vino a conocerse como dislocación de tornillo, de hélice o de tirabuzón (Burgers, 1940) (véase figura 7.9).

Luego de 1945, el desarrollo de la teoría y la obtención de evidencias fehacientes de su importancia sentaron formalmente las bases de la interpretación de la deformación y el endurecimiento de los metales como consecuencia de la presencia y el comportamiento de las dislocaciones; esto es lo que se pretende exponer en este capítulo.

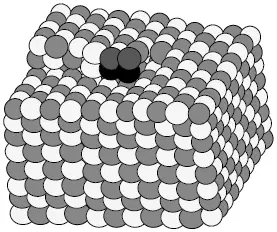
Figura 7.9 Dislocación de tornillo propuesta por Burgers

7.3. Modelos de dislocaciones

En realidad, en los cristales reales existen imperfecciones o “defectos” puntuales, lineales, superficiales o volumétricos. En este capítulo se tratan las imperfecciones de línea o dislocaciones, y se introduce el tema de las imperfecciones de superficie, como los límites de grano. Los otros tipos de defectos se desarrollan posteriormente.

Se entiende entonces que una dislocación es un defecto de línea en la red cristalina, el cual define la frontera entre la porción deslizada y la no deslizada del cristal. En general, una dislocación tiene dos componentes: una de borde y otra de tornillo. La dislocación de borde está definida por el borde del semiplano extra de átomos mostrado en la figura 7.10, que se presenta tridimensionalmente en la figura 7.11.

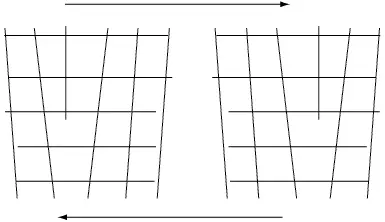
Figura 7.10 Dislocación de borde

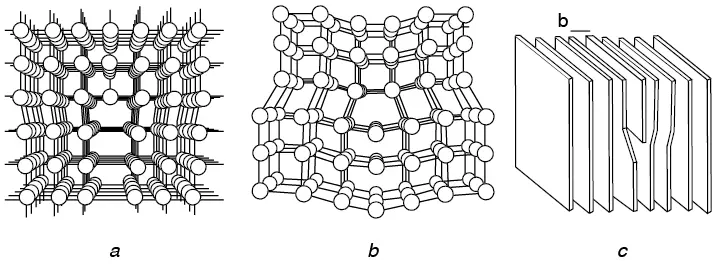
Figura 7.11 Modelos de dislocaciones de borde

7.3.1. Dislocación de borde

En la figura 7.11 se muestran modelos de dislocaciones. Estos esquemas son instructivos especialmente para las discusiones posteriores. Téngase en cuenta que las dislocaciones reales no se forman de esta manera, pero los resultados físicos causados por su existencia se pueden ilustrar con estos modelos.

Continuando con la figura 7.11, como resultado del semiplano extra, la parte superior del cristal está comprimida, mientras que la región que queda por debajo de la dislocación experimenta una dilatación. Por convención, el borde inferior del semiplano mostrado en la figura 7.11a es una dislocación de borde positiva y se representa con una T invertida (el símbolo ┴). Si el semiplano extra se introduce en la mitad inferior, las regiones de compresión y tracción se intercambian (véase figura 7.11b), y la línea de dislocación es una dislocación de borde negativa representada por el símbolo ┬. Es evidente que si una dislocación de borde positiva se encuentra con una negativa en el mismo plano, al combinarse forman un plano completo y se aniquilan mutuamente, eliminando las dos regiones de alta energía de distorsión de la red.

7.3.2. Dislocación de tornillo

En la dislocación de tornillo, la imperfección no está constituida por un semiplano extra, sino que la introducción de la dislocación de tornillo hace que la red ya no esté constituida por un conjunto de planos discretos, sino por una superficie helicoidal continua, como se ilustra con el modelo de la figura 7.12, similar a una escalera en espiral.

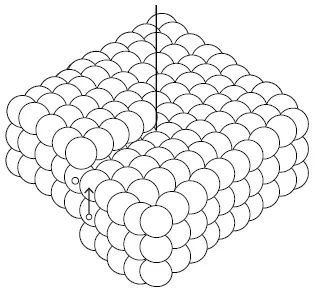
Figura 7.12 Modelo de bola dura de una dislocación de tornillo

Si en la figura 7.12 se mira en la dirección de la línea central indicada, después de una rotación de 360° se avanza una distancia reticular y el movimiento puede continuarse sobre la superficie helicoidal. En este caso, la rotación es como en un tornillo de rosca derecha y por eso la dislocación es una dislocación de hélice derecha; si el avance fuera al contrario sería una dislocación de tornillo izquierda.

En la realidad, las dislocaciones tienen componentes de tornillo y de borde (véase figura 7.13).

Nótese, además, que, en la dislocación de borde, el cizallamiento es perpendicular a la línea de dislocación, y en la dislocación de tornillo, el cizallamiento es paralelo a la línea de dislocación. Cuando el cizallamiento no es paralelo ni perpendicular, sino inclinado, se obtiene una dislocación mixta, como se observa con más claridad en la figura 7.14.

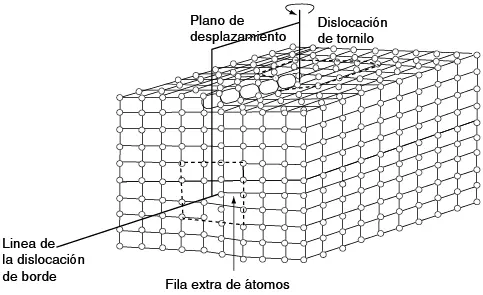
Figura 7.13 Una dislocación real con componente de tornillo y de borde

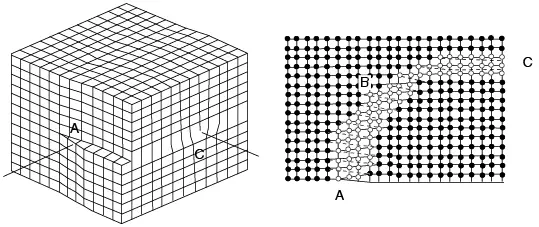
Figura 7.14 Dislocación mixta

7.3.3. Vector y circuito de Burgers

La definición más útil de una dislocación está dada en términos del Circuito de Burgers, que se traza según un procedimiento sugerido por Frederick Charles Frank (véase figura 7.15). Un circuito de Burgers es una serie de pasos, átomo a átomo, a lo largo de los vectores de la red, que genera una trayectoria cerrada alrededor de cualquier dislocación. Una trayectoria de este tipo se muestra en la figura 7.16, que empieza en S (start) y termina en F (finish). Si se hace la misma secuencia átomo a átomo en un cristal libre de dislocaciones, el circuito no se cierra (véase figura 7.16b). El vector requerido para cerrar el circuito y que va desde F a S en la figura 7.16b se define como vector de Burgers verdadero b. Como el sentido de circuito es el del tornillo de rosca derecha (RD), esta convención para el vector b se denomina convención FS/RD.