En el modelo de Orowan, la curva (que depende de los enlaces) se aproxima a una sinusoide, de modo que la tensión varía con la separación según la expresión
σ = Ksen(2π/λ) (x – a).
Orowan encontró que K era:
K = (E/π) (a/a0),
donde E es el módulo de elasticidad.
Así mismo,
a = π γ/σ,
donde γ es la tensión superficial del material.
De esta manera,
σmáx = K = (E/π) (a/a0) = Eγ/a0σ
o
σmáx = 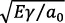
O sea que un material con resistencia teórica elevada debe tener un módulo de Young E elevado, alta energía de superficie γ y un espaciamiento entre átomos a0 pequeño.
En la tabla 7.1 se presentan las tensiones teóricas de clivaje para una serie de metales.
Tabla 7.1 Energía de superficie y tensión teórica de clivaje según el modelo de Orowan
| Material |
Dirección |
E(GPa) |
γ(mJ / m2) |
σmáx(GPa) |
σmáx / E |
| Fe-α |
100 |
132 |
2.000 |
30 |
0,23 |
| Fe-γ |
111 |
260 |
2.000 |
46 |
0,18 |
| Ag |
111 |
121 |
1.130 |
24 |
0,20 |
| Au |
111 |
110 |
1.350 |
27 |
0,25 |
| Cu |
111 |
92 |
1.650 |
39 |
0,20 |
| Cu |
100 |
67 |
1.650 |
25 |
0,38 |
| W |
100 |
39 |
3.000 |
86 |
0,22 |
| Diamante |
111 |
121 |
5.400 |
205 |
0,17 |
Fuente: Caddell (1980: 16).
Aunque los refinamientos del cálculo han disminuido los valores de la resistencia teórica, esta sigue siendo del mismo orden de magnitud mostrado en la tabla 7.1.
Por otra parte, Yakov Frenkel (conocido como J. Frenkel) (véase figura 7.3) realizó un cálculo de la tensión teórica de cizallamiento de un cristal estudiando dos planos de átomos en equilibrio, como se muestra en la figura 7.4. Cada átomo toca a sus vecinos, lo cual implica que un átomo como A descansa en el valle formado por B y C. Se supone que el deslizamiento ocurre cuando todos los átomos del plano D se muevan simultáneamente con respecto al plano E bajo la acción de una tensión aplicada τ.

Figura 7.3 Yakov Frenkel (1894-1952). Calculó la tensión teórica de cizallamiento de un cristal
Fuente: Evi (s. f.).
A medida que se aplica τ, manteniendo el plano E fijo por simplicidad, los átomos de D se desplazan en la dirección x. Si τ es pequeño, no sobrepasa las fuerzas de enlace y el desplazamiento es elástico: al retirar τ, los átomos vuelven a sus posiciones. Si la tensión cizallante causa un desplazamiento igual a b/2, cada átomo de D estará directamente encima y alineado con uno de E. Debido a la simetría si se retira τ, los átomos se moverán con la misma facilidad hacia la derecha o hacia la izquierda, para volver a la posición de equilibrio.
Por eso, cuando x = b/2, entonces τ = 0; y cuando x = b, se vuelve a la configuración inicial, pero todos los átomos de D se han deslizado una distancia b igual al diámetro del átomo. Para causar este desplazamiento se debe aplicar un valor τmáx entre los desplazamientos 0 < x < b/2. Es claro que la tensión cizallante necesaria para mover los átomos sobre el plano E varía periódicamente desde cero hasta un valor máximo τmáx.
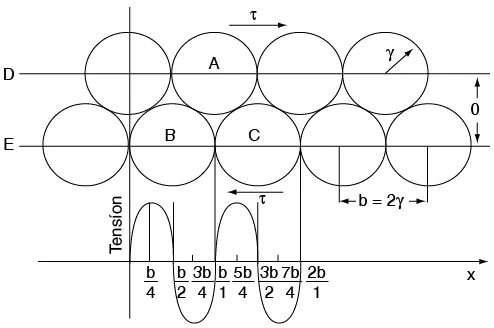
Figura 7.4 Tensión para cizallar un cristal ideal
Frenkel expresó la variación de τ con x como una función sinusoidal (aunque hay formas más exactas). En esencia:
τ = τmáx sen(2πx)/b, (7.1)
que se grafica en la figura 7.2b.
Si x = 0 o x = b/2, τ es cero; y si x = b/4, τ alcanza su máximo valor.
Para desplazamientos pequeños (x << b):
τ = τmáx (2πx)/b. (7.2)
Según la ley de Hooke, otra expresión para τ es:
τ = Gx/a,
donde G es el módulo de cizalladura y x/a es la deformación cortante.
Así, al igualar las ecuaciones 7.1 y 7.2 se tiene:
τmáx = Gb/2πa
τ = (Gb/2πa) sen(2πx/b) (7.3)
El valor máximo de τ representa la tensión a la cual se hace inestable la red y ocurre cuando x = b/4, o sea que:
τmáx = Gb/2πa ≈ τ0 (7.4)
donde τ0 es el esfuerzo cizallante crítico.
Para materiales cúbicos de cara centrada:
b = a0 / 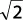 y a = a0 /
y a = a0 / 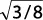 ,
,
siendo a0 = parámetro de la red. Así,
τmáx = G/5,4.
Los modelos más complejos dan valores de τmáx en las cercanías de G/30. Sin embargo, es instructivo comparar los valores teóricos calculados con la ecuación 7.4 con los valores de tensiones cizallantes determinados experimentalmente en monocristales de varios materiales, como se ve en la tabla 7.2.
Tabla 7.2 Tensiones de cedencia experimentales y teóricas (en cizalladura) de varios materiales
| Material |
G/2π (GPa) |
τexp, (Mpa) |
Error, τ0/τexp |
| Ag |
2,6 |
0,37 |
3 × 104 |
| Al |
11,3 |
0,78 |
1 × 104 |
| Cu |
19,6 |
0,49 |
4 × 104 |
| Ni |
32 |
3,2-7,35 |
1 × 104 |
| Fe |
33,9 |
27,5 |
1 × 103 |
| Mo |
54,1 |
71,6 |
8 × 102 |
| Mg (des. basal) |
7 |
0,39 |
2 × 104 |
| Mg (des. prism) |
7 |
39,2 |
2 × 102 |
| Ti (des. basal) |
16,9 |
13,7 |
1 × 103 |
Fuente: Meyers y Chawla (1982).
7.2. La necesidad de defectos: las dislocaciones
La conclusión inevitable de los trabajos teóricos esbozados fue que los modelos usados no representan el comportamiento de los cristales reales, los cuales contienen defectos que reducen su resistencia mecánica. En 1921, Alan Arnold Griffith (véase figura 7.5) postuló la presencia de grietas microscópicas para explicar la relativa debilidad de los sólidos frágiles como los vidrios, donde la tensión de fractura es muy inferior a la resistencia cohesiva máxima teórica. Este análisis originó lo que hoy se conoce como mecánica de la fractura, que es un enfoque mecánico-matemático de este problema.

Figura 7.5 Alan Arnold Griffith (1893-1963). Sus análisis originaron la mecánica de la fractura
Fuente: Suo (2006).

Figura 7.6 Teóricos de las dislocaciones. a. Michael Polanyi (1891-1976); b. Geoffrey Ingram Taylor (1886-1975); c. Vito Volterra (1860-1940).
Fuentes: Wikipedia (s. f. 4); Wikipedia (s. f. 9).
Otra manera de explicar la contradicción entre la teoría y la realidad de las dislocaciones fue postulada independientemente en 1934 por Michael Polanyi (véase figura 7.6a) y Egon Orowan en Alemania, y Geoffrey Ingram Taylor (véase figura 7.6b) en Inglaterra, introduciendo el concepto de dislocación, defecto este que permitiría que el plano D de la figura 7.4 se deslizara con niveles de tensión muchos más bajos (Hirth, 1985). Es de anotar que estas ideas ya habían sido esbozadas por el físico matemático italiano Vito Volterra en 1905 (véase figura 7.6c).
Читать дальше

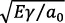


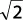 y a = a0 /
y a = a0 / 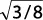 ,
,