En la figura 7.31 se observa el deslizamiento cruzado de un anillo de dislocaciones en un cristal fcc, donde la dislocación de tornillo se mueve en planos {111}, pero puede cambiar de un plano {111} a otro de la misma forma. En la figura 7.31, un pequeño anillo de dislocación con vector de Burgers b = (1/2) [1 ̅ 11] se está expandiendo en el plano (111) bajo la acción de un pequeño esfuerzo cizallante. Como se indicó en la figura 7.19, en w y en y, la dislocación es de borde puro positiva y negativa respectivamente, y en x y en z es de tornillo puro derecha e izquierda, en su orden. Supóngase que, en un momento determinado, la tensión cizallante que hace expandir el anillo tiende a mover la dislocación sobre el plano (11 ̅ 1) en vez de (111) (véase figura 7.31b). Como la dislocación de tornillo pura en z puede moverse libremente en el plano (11 ̅ 1) y se sigue expandiendo sobre él (véase figura 7.31c), cuando el anillo vuelve al plano original (111) se da un deslizamiento cruzado doble (véase figura 7.31d). Nótese que durante el movimiento de la dislocación sobre el plano de deslizamiento cruzado, solo se ha movido la componente de tornillo.
Las dislocaciones se mueven por deslizamiento a velocidades que dependen del esfuerzo cizallante aplicado, la pureza del cristal, la temperatura y el tipo de dislocación. Una relación empírica entre la velocidad y la tensión es:
v = v0 e(-A/τ),
donde v0 y A son constantes del material.
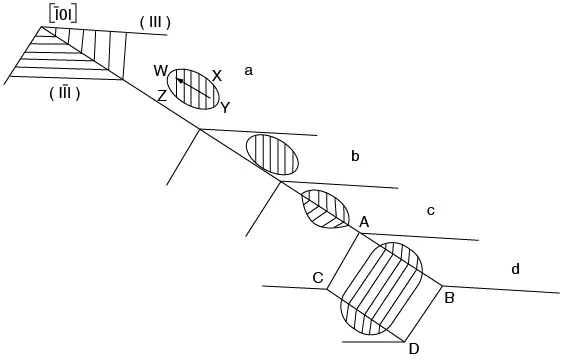
Figura 7.31 Deslizamiento cruzado en un cristal fcc. La dirección 101 es común a los planos (111) y (11).
7.5.3. Ascenso
En el deslizamiento normal, una dislocación de borde se mueve sobre un plano en la dirección del vector de Burgers, y en este solo toman parte pequeños desplazamientos localizados de filas de átomos, sobre dicho plano. Esto es lo que ocurre a temperaturas bajas cuando la difusión es difícil y no hay grandes concentraciones de defectos puntuales. Sin embargo, a temperaturas elevadas, una dislocación de borde puede moverse fuera de su plano de deslizamiento mediante el proceso de ascenso. Este movimiento implica la remoción de la fila de átomos que forman el borde del semiplano extra, típico de la dislocación de borde (véase figura 7.32).
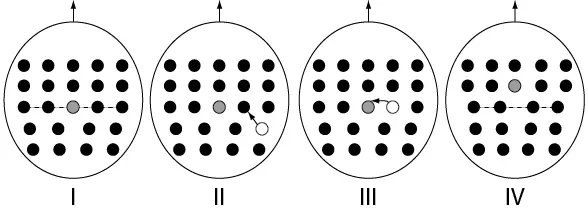
Figura 7.32 Ascenso de la dislocación de borde
Esto solo puede darse mediante la difusión de átomos hacia afuera de la dislocación, ya sea que vayan a lugares intersticiales o que las vacancias se difundan a estos lugares. Si se mueve la fila inferior normal al plano (véase figura 7.33b), la línea de dislocación asciende una distancia atómica (véase figura 7.33a); esto es un ascenso positivo. De manera similar, si se introduce una fila extra, la línea de dislocación se mueve hacia abajo una distancia atómica (véase figura 7.33c); esto es ascenso negativo. Este movimiento depende de la difusión y, por tanto, de la energía suministrada generalmente a modo de activación térmica. A temperatura elevada es muy importante esta forma de movimiento no conservativo.
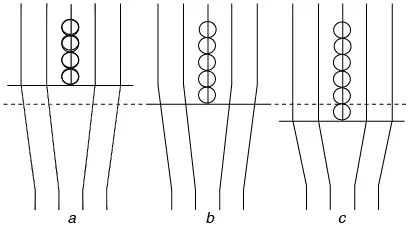
Figura 7.33 Ascenso positivo (a) y negativo (c) de la dislocación en (b)
7.5.4. Interacción dislocación-dislocación: escalones y pliegues
La forma más simple de deformación plástica comprende el movimiento de dislocaciones sobre un conjunto de planos paralelos; pero, en la práctica, las dislocaciones se generan y mueven simultáneamente en más de un sistema de deslizamiento. En estas circunstancias, las dislocaciones situadas en diferentes sistemas deben cortarse unas con otras, con cambios predecibles en la geometría. En la figura 7.34 se muestran dos intersecciones diferentes entre dislocaciones de cuña. En el primer caso (véase figura 7.34a), donde los vectores de Burgers son perpendiculares, la intersección de la dislocación AB lleva a un simple alargamiento de la dislocación XY. Por otro lado, la dislocación XY con vector de Burgers 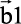 corta la dislocación AB, produciendo el escalón PP’ (jog), que tiene una longitud igual a
corta la dislocación AB, produciendo el escalón PP’ (jog), que tiene una longitud igual a 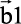 . El vector de Burgers de PP’ es, sin embargo,
. El vector de Burgers de PP’ es, sin embargo, 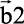 —el mismo de la dislocación a la cual pertenece—. Como
—el mismo de la dislocación a la cual pertenece—. Como 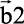 y PP’ son perpendiculares entre sí, el escalón PP’ es de tipo de borde. Se puede demostrar que este escalón no impide el movimiento de la dislocación AB.
y PP’ son perpendiculares entre sí, el escalón PP’ es de tipo de borde. Se puede demostrar que este escalón no impide el movimiento de la dislocación AB.
Cuando los vectores de las dislocaciones de cuña que se intersectan son paralelos, los escalones producidos son de naturaleza diferente. Como se ve en la figura 7.34b, la dislocación XY, con su vector de Burgers 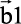 , produce un escalón en la dislocación AB. Como el vector de Burgers
, produce un escalón en la dislocación AB. Como el vector de Burgers 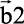 de la dislocación AB es paralelo al escalón PP’, el escalón es del tipo de hélice. Del mismo modo, el escalón QQ’ en la dislocación XY también es de tornillo. Los escalones de hélice PP’ y QQ’ tienen mayor movilidad que las dislocaciones a las cuales pertenecen, y por ello su presencia no obstaculiza el movimiento general de la dislocación.
de la dislocación AB es paralelo al escalón PP’, el escalón es del tipo de hélice. Del mismo modo, el escalón QQ’ en la dislocación XY también es de tornillo. Los escalones de hélice PP’ y QQ’ tienen mayor movilidad que las dislocaciones a las cuales pertenecen, y por ello su presencia no obstaculiza el movimiento general de la dislocación.
En resumen, los escalones generados en las dislocaciones de borde no afectan el movimiento de ellas. En la figura 7.35 se ve una síntesis de los tipos de pliegues y escalones que resultan de la interacción dislocación-dislocación.
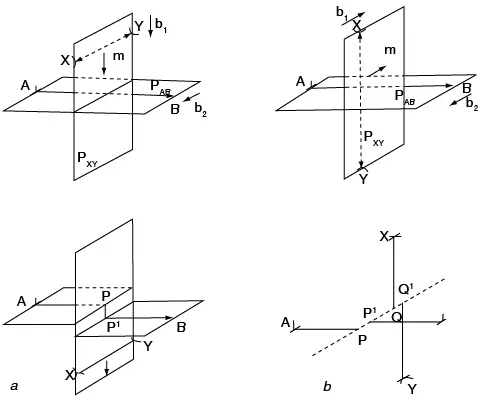
Figura 7.34 Intersección de las dislocaciones de cuña. a. Los vectores de Burgers son perpendiculares y producen un escalón de borde PP’ en la dislocación AB; b. los vectores son paralelos y producen dos escalones de tornillo PP’ y QQ’.
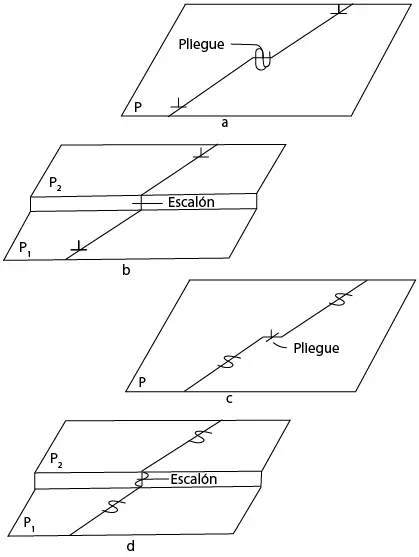
Figura 7.35 Interacción dislocación-dislocación: escalones y pliegues. a. pliegue de hélice; b. escalón de cuña; c. pliegue de cuña; d. escalón de hélice.
Lo establecido arriba no es aplicable cuando la intersección incluye dislocaciones de tornillo. Como se ve en la figura 7.36a, la intersección de una dislocación de borde y una de tornillo produce un escalón PP’ en la dislocación de cuña AB y otro escalón QQ’ en la de tornillo XY.
Puesto que cada escalón asume el mismo vector de Burgers de su dislocación, se puede ver que PP’ y QQ’ son ambos escalones de borde. Como se anotó, PP’ no impedirá el movimiento de la dislocación AB, mientras que QQ’ restringirá el movimiento de la dislocación de tornillo XY. Lo mismo puede decirse de los escalones de borde PP’ y QQ’ que se ven en las dislocaciones de hélice AB y XY en la figura 7.36b. La restricción colocada en la movilidad de las dislocaciones de tornillo se debe a que el escalón de borde solo puede moverse sobre el plano que contenga a QQ’ y 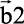 (es decir, el plano QQ’ YZ de la figura 7.37). Por consiguiente, cuando se aplica una tensión cizallante paralela a
(es decir, el plano QQ’ YZ de la figura 7.37). Por consiguiente, cuando se aplica una tensión cizallante paralela a 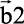 , los segmentos de tornillo XQ y Q’Y producirán desplazamientos paralelos a dicho vector, mientras las líneas de dislocación de tornillo se mueven a DE y FG respectivamente.
, los segmentos de tornillo XQ y Q’Y producirán desplazamientos paralelos a dicho vector, mientras las líneas de dislocación de tornillo se mueven a DE y FG respectivamente.
Читать дальше




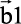 corta la dislocación AB, produciendo el escalón PP’ (jog), que tiene una longitud igual a
corta la dislocación AB, produciendo el escalón PP’ (jog), que tiene una longitud igual a 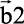 —el mismo de la dislocación a la cual pertenece—. Como
—el mismo de la dislocación a la cual pertenece—. Como