Ramón Guerrero Pérez - Electrotecnia. ENAE0108

I 1= I 2+ I 3

Recuerde

Un nudo es una zona del circuito eléctrico donde se unen más de dos conductores.

2ª Ley de Kirchhoff

Esta ley refleja lo siguiente:

La suma de las caídas de tensión (V) en los elementos que conforman una malla, es igual a la suma de las fuerzas electromotrices producidas por los generadores.

Siendo una malla cualquiera alimentada por un generador que suministra al circuito una tensión V G, las caídas de tensión en los n elementos que conforman la malla verifican la expresión:

V G= V 1+ V 2+ ... + V n

La Ley de Joule

Se denomina efecto Jouleal calentamiento producido por un elemento cuando es recorrido por una corriente eléctrica. Este calentamiento produce una disipación de energía (E) que se puede calcular mediante la expresión [siendo E la energía (en J) disipada por una resistencia, I la intensidad que circula por ella y V su valor de tensión]:

E = V · I

Esta ley se puede expresar en función de otras magnitudes como la potencia (P), el tiempo(t), la carga eléctrica (q), etc.:

E = q · V; E = P · t ...

Recuerde

Cuando entre los extremos de una resistencia se aplica una tensión, aparece una corriente eléctrica cuya intensidad es igual al cociente entre la tensión y el valor de la resistencia.

Aplicación práctica

Tras analizar el siguiente circuito de corriente continua formado por 3 resistencias (R1= 2Ω; R2 = 3 Ω; R3 = 4 Ω) conectadas en serie a una pila de 12 V (VG = 12 V).

1 Calcule la intensidad que pasa por las resistencias.

2 Calcule la caída de tensión de las resistencias.

3 Calcule la energía disipada por cada elemento.

SOLUCIÓN

1 Cálculo de la intensidad que pasa por las resistencias:Para calcular la intensidad que suministra la pila, se determina la resistencia equivalente que conforman R1, R2 y R3 (serie).Requ = R1 + R2 + R3;Requ = 2 + 3 + 4;Requ = 9ΩA continuación, se aplica la Ley de Ohm para calcular la intensidad que recorre el circuito:IG = VG / Requ ;IG = 12 / 9 ;IG = 1,33 AAl no existir nudos (bifurcaciones), la intensidad que suministra la pila (IG) es la misma que pasa por todas las resistencias (IG=IR1= IR2= IR2).1,33 = IR1 = IR2 = IR2;

2 Cálculo de la caída de tensión de las resistencias:Al conocer la intensidad que pasa por cada resistencia, se puede calcular, a partir de la Ley de Ohm, la caída de tensión de cada una de ellas (resultados redondeados):VR1 = IR1 · R1; VR1 = 1,33 · 2; VR1 = 2,67 V;VR2 = IR2 · R2; VR2 = 1,33 · 3; VR2 = 4 V;VR3 = IR3 · R3; VR3 = 1,33 · 4; VR3 = 5,33 V;Comprobación de que se verifica la 2ª Ley de Kirchhoff:VG = VR1 + VR2 + VR3;12 = 2,67 + 4 + 5,33;12 V = 12 V;

3 Cálculo de la energía disipada por cada elemento:Aplicando la Ley de Joule se puede calcular la energía disipada por la pila (EG) y por las tres resistencias (ER1 , ER2 , ER3):EG = VG · IG; EG = 12 · 1,33; EG = 15,96 JER1 = VR1 · IR1; ER1 = 2,67 · 1,33; ER1 = 3,55 JER2 = VR2 · IR2; ER2= 4 · 1,33; ER2 = 5,32 JER3 = VR3 · IR3; ER3 = 5,33 · 1.33; ER3 = 7,08 J

Los circuitos eléctricos representan la interconexión de dispositivos tales como generadores, interruptores, receptores etc., destinados a realizar una función específica.

A la hora de diseñar un circuito eléctrico existen varias configuraciones básicas, como: configuración en serie, configuración en paralelo y configuración estrella y triángulo.

Los componentes de estos circuitos eléctricos están sometidos a numerosos factores y comportamientos definidos por la propia naturaleza del componente y por una serie de leyes (Ohm, Kirchhoff, etc.) que permiten el análisis y estudio de estos conexionados.

Ejercicios de repaso y autoevaluación

1. Una corriente trifásica es:

1 Una señal continua senoidal.

2 Un tipo de corriente eléctrica usada en circuitos de pequeña escala.

3 Un conjunto de tres señales alternas desfasadas.

4 Un conjunto de tres señales alternas sin desfase.

2. La magnitud XL representa...

1 ... la intensidad que circula en un conductor.

2 ... la resistencia equivalente de varias resistencias conectadas en paralelo.

3 ... la impedancia de una bobina.

4 ... la resistencia equivalente de varias resistencias conectadas en serie.

3. Complete la siguiente frase:

La caída de tensión en una resistencia es mayor cuanto más elevadas sean, tanto la intensidad que circula por ella como el valor _________ que presente.

4. Relacione los siguientes elementos:

1 Ley de Joule

2 Ley de Ohm

3 Leyes de Kirchhoff

1 Potencia disipada

2 Intensidades entrantes y salientes en nudos

3 Relación tensión, intensidad, resistencia

4 Tensiones en mallas

5. Calcule la caída de tensión, la intensidad, y la energía de cada resistencia en el circuito de la figura:

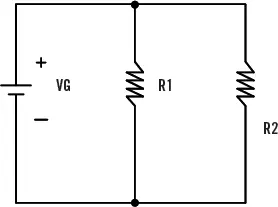
Donde: V G= 10 V; R 1= 5 Ω; R 2= 8 Ω

Notas:

1 Las resistencias están colocada en paralelo.

2 La intensidad que circula por todo el circuito no es la misma (existen 2 nudos).

3 Se pueden identificar dos mallas: la primera, formada por VG y R1, y la segunda, formada por VG y R2, por lo que la tensión de la pila (VG) es igual a la tensión de las dos resistencias.

Capítulo 4

Redes eléctricas de baja tensión

La energía eléctrica se utiliza tan habitualmente que parece que forma parte del entorno de modo natural, que siempre ha existido y existirá en beneficio de la gente.

Por este motivo, rara vez se tiene conciencia de la manera en la que este tipo de energía llega a los hogares. En este capítulo vamos a tratar los circuitos, las redes eléctricas y los componentes fundamentales que hacen posible la distribución de este tipo de energía.

La energía eléctrica es una forma de energía que tiene infinidad de aplicaciones: industrias, comercios, transporte, hogares, etc., caracterizándose principalmente por su controlabilidad, versatilidad y limpieza.

La energía eléctrica puede ser generada, de forma concentrada, en grandes cantidades, transmitiéndose a largas distancias a través de redes eléctricas. Antes de llegar a su destino, la electricidad es adaptada de forma fácil y eficaz dependiendo de la aplicación a la que esté destinada: iluminación, trabajo mecánico, etc.