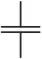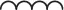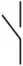Ramón Guerrero Pérez - Electrotecnia. ENAE0108

La configuración en serie consiste en la colocación de los elementos, uno a continuación del otro, donde el terminal de salida de un dispositivo se conecta al terminal de entrada del dispositivo siguiente.

Aplicación práctica

Calcule la resistencia equivalente de un conjunto de resistencias conectadas en paralelo de valores: R1 = 5 Ω, R2 = 15 Ω y R3 = 20 Ω.

SOLUCIÓN

Al estar conectadas en paralelo, se verifica que:

1/Requ = 1 / R1 + 1 / R2 + 1 / R3;

Entonces:

1/Requ = 1 / 5 + 1 / 15 + 1 / 20;

1/Requ = 0,2 + 0,07 + 0,05;

1/Requ = 0,32;

Despejando R equse tiene:

Requ = 1 / 0,32;

Requ = 3,13 Ω

Configuración estrella y triángulo

Cuando se conectan elementos en estrella,todos estos tienen un extremo unido a un punto común, mientras que el otro extremo queda libre para conectarse a otras partes del circuito.

En la conexión en triángulo,se van uniendo entre sí los extremos inicial y final de los distintos elementos. Estas uniones son las que se conectan a otras partes del circuito.

Estas configuraciones se usan fundamentalmente en el arranque de motores trifásicos. Estos motores requieren una mayor intensidad de corriente cuando comienzan su funcionamiento, usándose la configuración en estrella para este cometido (conectándola al circuito de arranque del motor). Una vez arrancado, el motor ya no necesita tanta corriente para funcionar, por lo que se produce un “cambio” (mediante una serie de mecanismos automáticos) a la configuración en triángulo para así evitar sobrecalentamientos en la máquina. Esto es lo que se denomina como arranque estrellatriángulo.

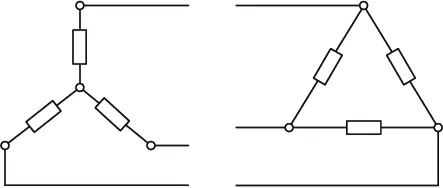
A continuación, se muestra un esquema de tres cargas conectadas en estrella (izquierda) y en triángulo (derecha).

Recuerde

En la configuración de estrella, todos los elementos tienen un extremo unido a un punto común, mientras que el otro extremo queda libre para conectarse a otras partes del circuito.

La representación gráfica de circuitos eléctricos es una importante ayuda para analizarlos y estudiar los problemas que se puedan presentar a la hora de hacer los cálculos necesarios. Cada dispositivo eléctrico que existe tiene su propia simbología, la cual, es fundamental para la representación y análisis de un circuito o partes del mismo.

A continuación, se muestra una tabla con la representación gráfica, según la normativa, de los dispositivos más usados en el análisis y cálculo de circuitos eléctricos:

Símbolo	Elemento	Notas
	Conductor
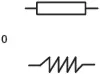	Resistencia
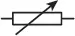	Potenciómetro o resistencia variable	Resistencia de valor variable
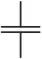	Condensador
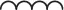	Bobina
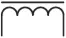	Bobina con núcleo magnético
	Máquina	En el centro del símbolo puede presentar una letra que indique la naturaleza de la máquina. G: Generador; M: Motor, etc.
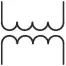	Transformador	Se pueden representar las polaridades con puntos
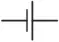	Pila o acumulador
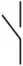	Interruptor abierto
	Interruptor cerrado
	Voltímetro	Aparato de medida

En este apartado se verán algunos principios básicos a tener en cuenta a la hora de analizar un circuito en corriente continua. Al final del capítulo se propone resolver un circuito muy sencillo, donde se deben aplicar algunos de los teoremas enunciados previamente.

Pero antes de proceder a estudiar el análisis de circuitos eléctricos, es necesario conocer algunos conceptos básicos:

1 Nudo: un nudo es una zona del circuito eléctrico donde se unen más de dos conductores.

2 Rama: parte de un circuito comprendida entre dos nudos próximos.

3 Malla: conjunto de ramas que forman un “camino” cerrado.

Para poder determinar cualquier variable presente en un circuito eléctrico (como puede ser la tensión, intensidad, potencia, etc.) es fundamental conocer algunas leyes fundamentales que los gobiernan. Estas leyes constituyen la base sobre la que se apoya el análisis de circuitos eléctricos.

La Ley de Ohm

Esta ley se enuncia de la siguiente forma:

Cuando entre los extremos de una resistencia se aplica una tensión, aparece una corriente eléctrica cuya intensidad es igual al cociente entre la tensión y el valor de la resistencia.

Matemáticamente, esta ley se expresa como:

V = I · R( R = V / I; I = V / R )

Las Leyes de Kirchhoff

Las leyes Kirchoff son dos enunciados basados en el teorema de conservación de energía. Son las dos leyes más utilizadas en la electrónica, ya que son la base del análisis de circuitos eléctricos.

1ª Ley de Kirchhoff

Esta ley indica lo siguiente:

En un nudo, la suma de las intensidades que entran es igual a la suma de las intensidades que salen.

Siendo un nudo cualquiera, si I 1es una intensidad que entra en un nudo y I 2e I 3son salientes, se verifica que: