1 ...6 7 8 10 11 12 ...17 •3,03003000300003... Se trata de un número con infinitas cifras decimales, pero que ¡no es periódico!
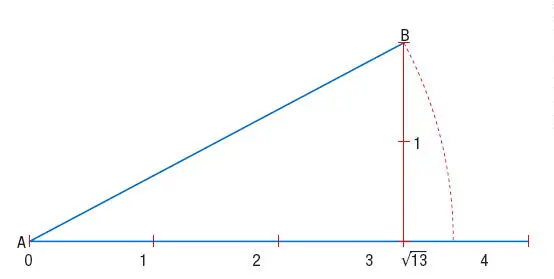
•El resultado de efectuar una raíz no exacta, como por ejemplo 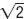 = 1,4142… Sus cifras decimales se repiten, pero no de forma periódica, sino al azar.
= 1,4142… Sus cifras decimales se repiten, pero no de forma periódica, sino al azar.
•El resultado de dividir la longitud de una circunferencia entre la longitud de su diámetro, es un número al que designamos habitualmente con la letra griega π y cuyo valor es: π = 3,14159…
La conclusión es clara: los números racionales no son suficientes si deseamos efectuar todas las operaciones habituales, en particular la radicación. Necesitamos introducir un nuevo conjunto de números con infinitas cifras decimales no periódicas, a los que llamaremos irracionales.
EL NÚMERO ÁUREO
Históricamente hablando, el primer número irracional conocido fue el número  cuyo valor es: 1,6180339…
cuyo valor es: 1,6180339…
Se obtiene al dividir las longitudes de la diagonal de un pentágono regular y el lado del mismo.
El teorema de Pitágoras permite dibujar en la recta algunos números irracionales. Para representar el número 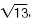 por ejemplo, tomamos tres unidades. A continuación, en una recta perpendicular, tomamos dos. Finalmente, utilizando un compás, trasladamos a la recta la longitud AB , que mide:
por ejemplo, tomamos tres unidades. A continuación, en una recta perpendicular, tomamos dos. Finalmente, utilizando un compás, trasladamos a la recta la longitud AB , que mide: 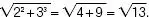
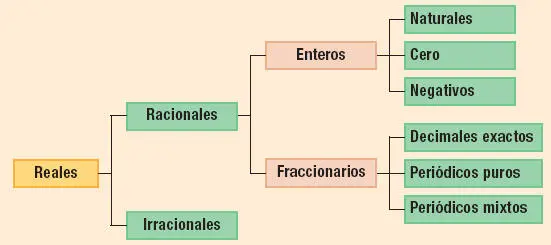
LOS NÚMEROS REALES
UN SISTEMA DE MEDIDA CASI UNIVERSAL
¿Te imaginas que en cada país, en cada región incluso, utilizásemos unidades de medida diferentes? ¡Vaya lío! Pues así sucedía hasta hace un poco más de doscientos años. En unas comarcas se medía en palmos; en otras, en varas; en otras, en pies, etc., hasta que en 1792 la Academia de Ciencias de París encargó a los científicos Delambre y Mechain la elaboración de un sistema único de medidas. Así nació el sistema métrico decimal, cuya unidad fundamental es el metro y que hoy se utiliza prácticamente en todo el mundo.
UNIDADES DE LONGITUD
Adela practica el atletismo. El próximo domingo correrá una carrera de 12,3 km. Si en cada zancada recorre 80 cm por término medio, ¿cuántas zancadas dará a lo largo de la carrera?
Para responder a esta pregunta transformaremos en primer lugar los kilómetros a centímetros:
12,3 km = 12,3 · 100.000 cm =1.230.000 cm. Por tanto,
el número de zancadas será: 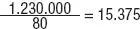 zancadas.
zancadas.


Antes de la implantación del sistema métrico decimal existía una gran diversidad de unidades y elementos para efectuar mediciones. Derecha, media fanega, medida castellana de capacidad para granos o legumbres; abajo, arroba de Girona, un peso de unas 25 libras, esto es, unos 11,502 kilogramos.
¿QUÉ ES MEDIR?
Para medir algo, lo primero que tenemos que hacer es definir una cantidad inicial que llamaremos unidad. Posteriormente, ya podremos medir una magnitud, comparándola con la unidad y viendo cuántas veces la contiene.
En el sistema métrico decimal se emplean los prefijos deca-, hecto-y kilo-para los múltiplos de la unidad.
En el sistema métrico decimal se emplean los prefijos deci-, centi-y mili-para los submúltiplos de la unidad.




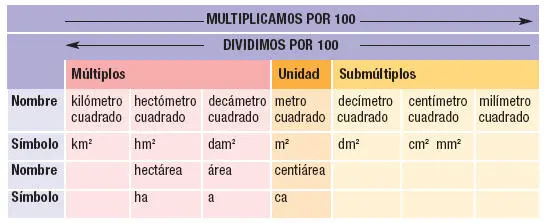
UNIDADES DE SUPERFICIE
A Lorenzo le encanta hacer comparaciones y se pasa el día calculando cosas mentalmente. Mientras tomaba el sol relajadamente al borde de una piscina de 813 m 3de capacidad, le han venido dos preguntas a la cabeza: ¿cuántas veces es mayor la capacidad de la piscina que la de una botella de vino de 75 cl? ¿Cuántas toneladas pesaría el agua de la piscina?
Las ha contestado fácilmente: 813 m 3= 813 · 1.000 dm 3= = 813.000 dm 3= 813.000 l = 813.000 · 100 cl = 81.300.000 cl 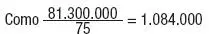
concluimos que la capacidad de la piscina es 1.084.000 veces mayor que la capacidad de la botella. Por otra parte, un litro de agua destilada pesa un kilo. Un litro de agua de piscina pesa un poco más, ya que, además de agua, contiene otras cosas, como sales, cloro, etc., pero podemos afirmar que pesaría aproximadamente 813.000 kg, es decir, 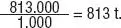
UNIDADES DE VOLUMEN, CAPACIDAD Y MASA
Lucía y Juan trabajaban en una finca de 27,3 ha, pero han decidido venderla a una constructora que dedicará 5 ha a zonas comunes y dividirá el resto en parcelas de 500 m 2destinadas a chalets. ¿Cuántos se edificarán?
La zona edificable mide: 27,3 – 5 = = 22,3 ha. Esta superficie equivale a: 22,3 · 10.000 = 223.000 m 2. Se podrán hacer: 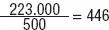 parcelas.
parcelas.

Como en el terreno informático se emplea la base dos y la potencia de dos más cercana a mil es 2 10= 1.024, un kilobyte no equivale a 1.000 bytes, sino a 1.024 bytes, un megabyte a 1.024 · 1024 = 1.048.576 bytes y así sucesivamente.
Читать дальше

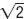 = 1,4142… Sus cifras decimales se repiten, pero no de forma periódica, sino al azar.
= 1,4142… Sus cifras decimales se repiten, pero no de forma periódica, sino al azar. cuyo valor es: 1,6180339…
cuyo valor es: 1,6180339…
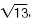 por ejemplo, tomamos tres unidades. A continuación, en una recta perpendicular, tomamos dos. Finalmente, utilizando un compás, trasladamos a la recta la longitud AB , que mide:
por ejemplo, tomamos tres unidades. A continuación, en una recta perpendicular, tomamos dos. Finalmente, utilizando un compás, trasladamos a la recta la longitud AB , que mide: 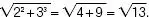

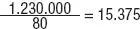 zancadas.
zancadas.






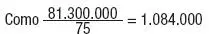
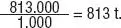
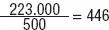 parcelas.
parcelas.











