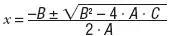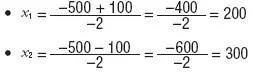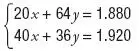1 ...8 9 10 12 13 14 ...17 
Los matemáticos griegos anteriores a Diofante de Alejandría (siglo III d.C.) no empleaban el álgebra pero, gracias a su gran ingenio, llegaron a plantear y resolver ecuaciones e identidades por procedimientos geométricos. Por ejemplo, la identidad: ( a + b ) 2= a 2+ b 2+ 2 ab . En la fotografía, templo griego en Selinunte (Sicilia).
LA ECUACIÓN DE SEGUNDO GRADO

El ayuntamiento de una localidad quiere destinar una parte de un terreno a la construcción de un parque rectangular. Su superficie ha de ser 60.000 m 2y su perímetro, es decir, la suma de las longitudes de sus lados, 1.000 m. ¿Cuáles tienen que ser las dimensiones de dicho parque?
Para plantear este problema hay que tener en cuenta que los dos lados diferentes del rectángulo tienen que sumar 500 m, ya que constituyen juntos la mitad del perímetro. Por tanto, si llamamos x a uno de ellos, el otro será 500 – x .
Por otra parte, la superficie de un rectángulo se obtiene multiplicando sus dos dimensiones. Por consiguiente: x (500 – x ) = 60.000.
Eliminando el paréntesis, obtenemos finalmente una ecuación de segundo grado: 500 x – x 2= 60.000.
Si dos cosas son iguales, su diferencia es cero: 500 x – x 2– 60.000 = 0.
La ecuación de segundo grado se suele escribir comenzando por el término de segundo grado: – x 2+ 500 x – 60.000 = 0.
En una identidad no tiene sentido calcular el valor de las incógnitas, ya que una identidad se cumple para cualquier valor. Si intentamos hacerlo ocurre lo siguiente:
2 x + x = 3 x ⇒ 3 x = 3 x ⇒ 3 x – 3 x = 0 ⇒ 0 = 0
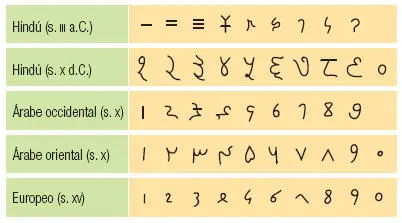
EVOLUCIÓN DE LOS SISTEMAS DE NUMERACIÓN
Una ecuación de segundo grado es una expresión que se puede reducir a la forma: A x 2+ B x + C = = 0, donde A , B y C son números reales y A no vale cero, ya que, si así fuese, la ecuación sería de primer grado.
La palabra álgebraderiva de Al-gabr , título de una obra del matemático árabe al-Hwarizmi escrita en el siglo noveno de nuestra era.
RESOLUCIÓN DE LA ECUACIÓN DE SEGUNDO GRADO
Para obtener las soluciones de nuestro problema podemos ir tanteando con todas las parejas de números que sumen 500, hasta encontrar una cuyo producto sea 60.000, pero acabaremos mucho antes si aplicamos la fórmula:
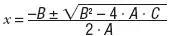
Como en nuestro caso A = – 1, B = 500 y C = – 60.000, tendremos:

La ecuación tiene pues dos posibles soluciones:
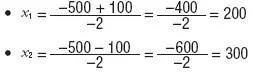

En Europa, el álgebra se desarrolló en la época del Renacimiento, gracias sobre todo a los matemáticos italianos Tartaglia (a la izquierda) y Cardano (a la derecha) y al francés Viète.

Fachada de las Escuelas Mayores, de estilo renacentista, en Salamanca (España).
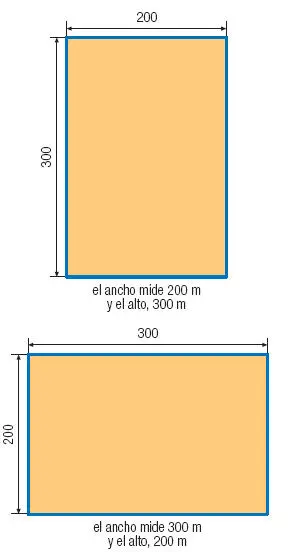
Las dos soluciones de la ecuación significan lo siguiente: como los dos lados suman 500 m, podremos orientar el parque de dos maneras.
Se llama discriminante de una ecuación de segundo grado a la expresión: B 2– 4 · A · C . Según sea el discriminante, la ecuación tendrá una solución, dos o ninguna.
| Discriminante |
Número de soluciones |
Motivo |
| Positivo |
Dos |
De la raíz cuadrada de un número positivo se obtienen dos resultados opuestos. |
| Cero |
Una |
La raíz cuadrada de cero tiene un único resultado: cero. |
| Negativo |
Ninguna |
No existe ningún número real que elevado al cuadrado dé negativo. Por tanto, en este caso, la raíz no tiene ninguna solución. |
SISTEMAS DE ECUACIONES
Laura es fontanera. Debido a la escasez de este tipo de profesionales, frecuentemente tiene que efectuar reparaciones en ciudades cercanas. La primera semana de abril ha trabajado 20 horas en viviendas situadas fuera de su localidad y 64 en su ciudad y ha ganado 1.880 euros en total, mientras que la segunda semana ha trabajado 40 fuera y 36 en su ciudad, ganando 1.920 euros. ¿Sabrías calcular a cuánto cobra cada hora en su ciudad y cada hora en las localidades vecinas?
PLANTEAMIENTO
Tenemos que contestar a dos preguntas, por tanto, utilizaremos dos incógnitas:
x = precio de una hora de trabajo en otra localidad; y = precio de una hora de trabajo en su ciudad.
Multiplicando las horas trabajadas por el precio de cada hora, podemos calcular lo que ganó en la primera semana de abril: 20 x + 64 y = 1.880.
De la misma forma, calculamos lo que ganó la segunda semana: 40 x + 36 y = 1.920.
Tenemos que buscar el valor de las incógnitas para que se cumplan ambas ecuaciones. Entonces decimos que estamos trabajando con un sistemade dos ecuaciones con dos incógnitas y lo escribimos así:
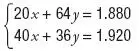
UNA MATRIZ ES UN CONJUNTO DE NÚMEROS ORDENADOS POR FILAS Y COLUMNAS
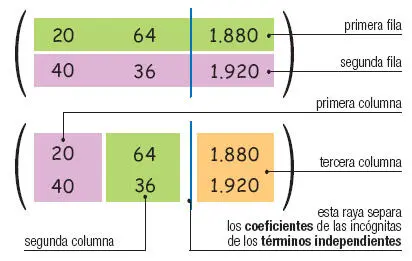
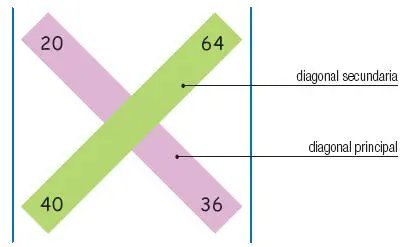

Para calcular el valor del determinante de orden 2 comenzamos multiplicando los números de la diagonal principal. A continuación, multiplicamos los números de la diagonal secundaria. Por último, restamos ambos resultados.
Читать дальше