Equipo Parramón Paidotribo - Matemáticas y Física & Química

MÉTODO DE CRAMER

PREPARANDO LAS VACACIONES

Álex está preparando sus próximas vacaciones. Ha realizado una consulta a través de Internet y ha averiguado que un hotel de la costa tiene treinta habitaciones, algunas de ellas dobles y otras sencillas, y que dispone de cuarenta camas en total. Álex se pregunta qué cantidad de habitaciones de cada tipo tiene el hotel. ¿Sabrías contestar a su pregunta?

Al restar diez a los dos miembros de la ecuación, da la sensación de que el diez desaparece de la izquierda de la igualdad y aparece a la derecha. Por eso se dice que si un término está sumando en uno de los miembros de la ecuación, puede pasar al otro miembro restando y viceversa.

A través de Internet, Álex está intentando averiguar el número de habitaciones de los distintos hoteles.

MÉTODO DE REDUCCIÓN

Llamando x al número de habitaciones sencillas e y al número de habitaciones dobles, obtenemos el sistema siguiente:

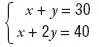
La Introducción al análisis de las curvas algebraicas , publicada en 1750 por el matemático suizo Gabriel Cramer (1704-1752), constituye uno de los primeros tratados de geometría analítica.

El método de reducción, también llamado método de Gauss, consiste en eliminar una de las incógnitas. Con este fin, damos los pasos siguientes:

•Multiplicamos por –1 a la primera ecuación: – x – y = – 30.

•Sumamos las dos ecuaciones:

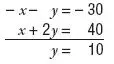
•Sustituimos el valor obtenido en la primera ecuación: x + 10 = 30, para resolver esta ecuación restamos 10 a cada miembro: x + 10 – 10 = 30 – 10, es decir: x = 30 – 10 y finalmente x = 20.

El hotel tiene, por consiguiente, veinte habitaciones sencillas y diez dobles.

BUENAS ACCIONES

Pedro ha invertido un total de 200.000 euros en la compra de acciones de dos empresas. El año pasado las acciones de la primera empresa le proporcionaron unas ganancias equivalentes a la quinta parte de lo invertido y las de la segunda le rentaron una sexta parte. En total ganó 36.000 euros. Calcula el dinero invertido en cada una.

La bolsa es el mercado en el que se efectúan transacciones sobre valores mobiliarios o de mercancías.

MÉTODO DE SUSTITUCIÓN

Llamando x al dinero invertido en la primera empresa e y a la cantidad invertida en la segunda, obtenemos el sistema siguiente:

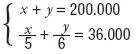
Si multiplicamos la segunda ecuación por 30, que es el mínimo común múltiplo de los denominadores, obtenemos:

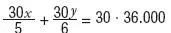
con lo que el sistema se convierte en:

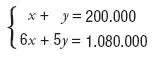
El método de sustitución consiste en:

•despejar una incógnita de la primera ecuación: y = 200.000 – x ,

•sustituirla en la segunda:

6 x + 5 (200.000 – x ) = 1.080.000.

Ahora sólo tenemos que resolver una ecuación con una incógnita.

Efectuamos el paréntesis:

6 x + 1.000.000 – 5 x = 1.080.000 es decir: x + 1.000.000 = 1.080.000,

y finalmente: x = 1.080.000 – 1.000.000 = = 80.000 euros.

Una vez obtenido el valor de una de las incógnitas, lo sustituimos para hallar el de la otra: y = 200.000 – x =

= 200.000 – 80.000 = 120.000 euros.

Luego Pedro invirtió 80.000 euros en una empresa y 120.000 en la otra.

Nunca está de más comprobar las soluciones de un sistema. En nuestro caso, la primera ecuación se cumple, ya que:

80.000 + 120.000 = 200.000

y la segunda también:

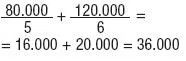
En buena parte, la marcha de la economía mundial se refleja en las bolsas. Las principales bolsas son: Nueva York, Londres, París, Frankfurt y Tokio.

LA FIESTA DE CUMPLEAÑOS

María y sus amigos celebraron el pasado sábado una fiesta de cumpleaños. Eran cuarenta en total. Al cabo de una hora se habían marchado diez chicos, por diversos motivos, con lo que el número de chicas pasó a ser el doble que el de chicos. ¿Cuántos chicos y chicas había en la fiesta inicialmente?

MÉTODO DE IGUALACIÓN

Llamando x al número de chicas e y al de chicos de la fiesta,

obtenemos el sistema siguiente: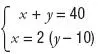

El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones. Como en este caso, ya tenemos despejada la x en la segunda ecuación, despejaremos esa misma incógnita en la primera, con lo que el sistema resultante

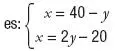
Ahora igualamos los dos valores:

40 – y = 2 y – 20.

Si agrupamos las incógnitas, resulta:

– y – 2 y = – 20 – 40 es decir: –3 y = – 60.

Dividimos entre –3 a la ecuación:

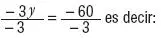
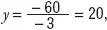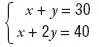
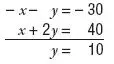
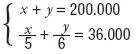
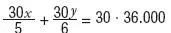
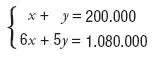
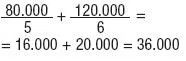
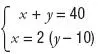
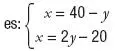
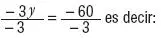
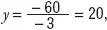por lo tanto,