1 ...7 8 9 11 12 13 ...17 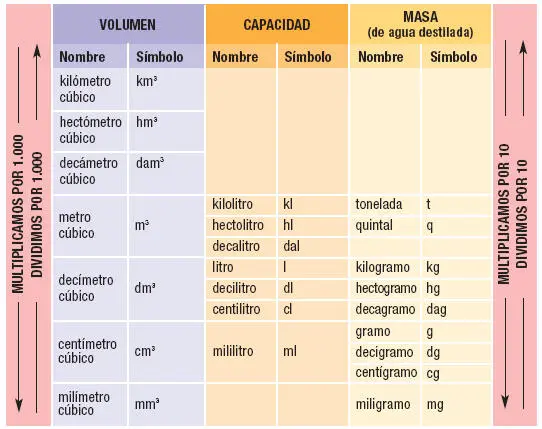
Para medir grandes magnitudes se utilizan los prefijos mega (M), que equivale a un millón, giga (G), que equivale a mil millones, y tera (T), equivalente a un billón. La informática ha popularizado estos múltiplos de la unidad. Así, por ejemplo, hablamos de megahercios o gigabytes.

ECUACIONES
A Marcelo le han rebajado la décima parte del precio de una impresora, pero, al ir a pagar, le han cargado una décima parte en concepto de impuestos. Al final ha pagado 198 euros. ¿Sabrías calcular cuál era el precio inicial de la impresora?
LA BÚSQUEDA DE LAS INCÓGNITAS
Para plantear un problema, es conveniente dar los siguientes pasos:
1. Leer el enunciado despacio, tantas veces como sean necesarias para comprenderlo perfectamente.
2. Buscar qué nos preguntan. Generalmente, las preguntas están situadas al final del enunciado. En el problema que nos ocupa hay una única pregunta: el precio inicial de la impresora.
3. Emplear tantas letras, llamadas incógnitas, como cosas diferentes nos pregunten. En nuestro caso: x = precio inicial de la impresora.

La impresora de Marcelo.
Se llaman términosde una ecuación a cada uno de los sumandos que intervienen en ella. En nuestro ejemplo, el primer miembro tiene dos términos y el segundo, uno.
Una ecuación tiene dos miembros. Uno de ellos está situado a la izquierda del signo igual y el otro, a su derecha.


Las matemáticas tuvieron, tanto en el Egipto antiguo, como en la antigua Mesopotamia, un desarrollo asombroso. Ambos pueblos eran capaces de plantear y resolver ecuaciones. En las fotografías: izquierda, obelisco en Karnak (Egipto); derecha, la antigua ciudad mesopotámica de Mari (Siria).
PLANTEAMIENTO
Una vez localizas las incógnitas, hay que volver al principio del enunciado y separar las frases. En nuestro ejemplo hay tres ideas fundamentales:
•Le han rebajado la décima parte. Esto significa que ha pagado nueve décimas partes del precio inicial. Luego ha pagado: 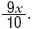
•Le han cargado una décima parte, es decir: 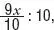 que equivale a
que equivale a 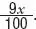
•Al final ha pagado 198 euros, esto es: 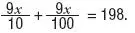
El gradode una ecuación es el mayor de los exponentes a los que está elevada la incógnita. La ecuación de nuestro ejemplo es de primer grado. Si el mayor exponente fuera un dos, se diría que es de segundo grado; si fuera un tres, de tercer grado y así sucesivamente.

El emperador Qin Shi Huangdi ordenó la destrucción de todos los libros de matemáticas en el año 213 a.C. Por este motivo no podemos saber con exactitud en qué momento los chinos comenzaron a trabajar con ecuaciones matemáticas.
RESOLUCIÓN
Resolver una ecuación consiste en encontrar el valor que hay que sustituir en la incógnita para que la igualdad se cumpla. Para alcanzar este objetivo, daremos los pasos siguientes:
1. Eliminamos los denominadores multiplicando toda la ecuación por el mínimo común múltiplo de dichos denominadores, en este caso cien: 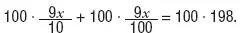
2. Efectuamos las operaciones y obtenemos: 90 x + 9 x = 19.800.
3. Agrupamos los términos que contienen a la incógnita: 99 x = 19.800.
4. Dividimos a toda la ecuación por noventa y nueve: 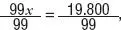 o lo que es lo mismo:
o lo que es lo mismo: 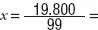 = 200 euros.
= 200 euros.
Podríamos haber pensado que, si a Marcelo le descuentan una décima parte del precio y después le cargan otra décima parte, el precio inicial y el final tendrían que ser iguales: 198 euros. Resolviendo matemáticamente el problema, hemos visto que este razonamiento intuitivo es falso.
Cuando a Marcelo le descuentan la décima parte de 200 euros, le descuentan 20 euros. La décima parte de recargo se hace pues sobre 180 euros y equivale a 18 euros. Por tanto, el descuento y el recargo no coinciden y el precio final es 180 + 18 = 198 euros.

En la India, las matemáticas fueron cultivadas por los sacerdotes, quienes aplicaban sus conocimientos geométricos para la construcción de los altares.
¿QUÉ ES UNA ECUACIÓN?
En una expresión algebraica intervienen números y letras. Pero, no toda expresión algebraica es una ecuación. A la vista del problema que hemos resuelto, podemos concluir que para que una expresión algebraica sea una ecuación, tiene que cumplir una serie de condiciones:
•Tiene que contener una igualdad. Así, por ejemplo, no es una ecuación la expresión: 2 x + 3 a + 5.
•Tiene que contener incógnitas. Por tanto, no sería una ecuación la expresión: 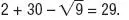
•La igualdad se tiene que cumplir solamente para algunos valores de las incógnitas, llamados soluciones. Por consiguiente, la expresión: 2 x + x = 3 x no es una ecuación, puesto que se cumple para cualquier valor que le demos a la incógnita. Este tipo de expresiones algebraicas reciben el nombre de identidades.
Читать дальше







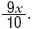
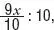 que equivale a
que equivale a 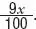
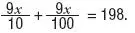

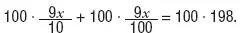
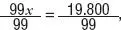 o lo que es lo mismo:
o lo que es lo mismo: 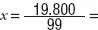 = 200 euros.
= 200 euros.