1 ...6 7 8 10 11 12 ...26 EXAMPLE 1.29.– The mapping 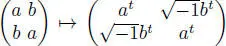 is a pseudoinvolution on Q ( n ).
is a pseudoinvolution on Q ( n ).
EXAMPLE 1.30.– The mapping 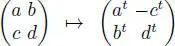 is a pseudoinvolution on Mm+n ( F ).
is a pseudoinvolution on Mm+n ( F ).
Replacing the involution ∗ in example 1.28with the pseudoinvolutions of examples 1.29and 1.30, we get unital Jordan bimodules over Mm+n ( F ), where m , n are odd, and over Q ( n ) (+).
THEOREM 1.7 (see Martin and Piard (1992), Martínez et al . (2010)).– An arbitrary irreducible Jordan bimodule over 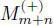 , m + n ≥ 3 or Q ( n ) (+), n ≥ 3, is one of examples 1.27and 1.28with an involution or a pseudoinvolution, or a regular bimodule.
, m + n ≥ 3 or Q ( n ) (+), n ≥ 3, is one of examples 1.27and 1.28with an involution or a pseudoinvolution, or a regular bimodule.
The exceptional Jordan superalgebra K 10has rank 3. Jordan bimodules over K 10have been classified by Shtern (1987).
THEOREM 1.8 (Shtern (1987)).– All Jordan bimodules over K 10are completely reducible. The only irreducible Jordan bimodules over K 10are the regular bimodule and its opposite.
1.7.2. Superalgebras of rank ≤ 2
If J is a Jordan superalgebra of rank ≤ 2, then, generally speaking, it is no longer true that its universal multiplicative algebra is finite dimensional and that any Jordan bimodule is completely reducible.
1.7.2(a)In the case J = Q (2) (+), however, it is true (see Martínez et al . (2010)). The universal multiplicative enveloping algebra U ( Q (2) (+)) is finite dimensional and semisimple and the description of irreducible Jordan bimodules is similar to that of Q ( n ) (+), n ≥ 3.
1.7.2(b)Let us discuss bimodules over Kantor superalgebras. Recall that the Kantor superalgebras Kan( n ) are Kantor doubles of the Grassmann superalgebras G ( n ), n ≥ 1, with respect to the Poisson bracket
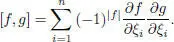
Let Kan( n ) = G ( n ) + G ( n ) v . The Grassmann superalgebra G ( n ) is embeddable in the associative commutative superalgebra A = F [ t, ξ 1,…, ξn ] = F [ t ] ⊗ F G ( n ).
For an arbitrary scalar α ∈ F , the Poisson bracket [ , ] extends to the Jordan bracket on A defined by [ t , ξi ] = 0, [ ξi , ξj ] = – δij , [ ξi , 1] = 0, [ t , 1] = αt . The Kantor double Kan( n ) = G ( n ) + G ( n ) v embeds in the Kantor double Kan( A , [ , ]) = A + Av . The subspace V ( α ) = tG ( n ) + tG ( n ) v is an irreducible unital Jordan bimodule over K ( n ). The square of the multiplication operator by the element v acts on V ( α ) as the scalar multiplication by α .
The simple superalgebras Kan( n ), n ≥ 2 are exceptional (see Martínez et al . (2001)). Therefore, they do not have non-zero one-sided Jordan bimodules.
THEOREM 1.9 (Stern (1995), Martínez and Zelmanov (2009), Solarte and Shestakov (2016)).– Every finite dimensional irreducible Jordan bimodule over Kan( n ), n ≥ 2 is isomorphic to V ( α ) or V ( α ) op, α ∈ F .
In Solarte and Shestakov (2016), the theorem above was proved for algebras over a field of characteristic p > 2.
1.7.2(c)Jordan superalgebras of a superform. Let 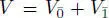 be a ℤ/2ℤ-graded vector space with a non-degenerate supersymmetric bilinear form. Assume
be a ℤ/2ℤ-graded vector space with a non-degenerate supersymmetric bilinear form. Assume 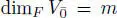 ,
, 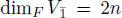 and choose a basis e 1,…, em in
and choose a basis e 1,…, em in 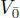 with 〈 ei , ej 〉 = δij and a basis v 1, w 1,…, vn , wn in
with 〈 ei , ej 〉 = δij and a basis v 1, w 1,…, vn , wn in 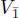 such that
such that
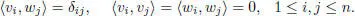
Let Cl( m ) be the Clifford algebra of the restriction of the form 〈 , 〉 to 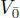 , and let
, and let
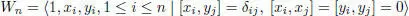
be the simple Weyl algebra.
Then the tensor product S = Cl( m ) ⊗ F Wn is the universal associative enveloping superalgebra of the Jordan superalgebra J = V + F ∙ 1.
Since the algebra Wn , n ≥ 1 is infinite dimensional, it follows that the superalgebra J does not have non-zero finite dimensional one-sided Jordan bimodules unless n = 0.
Consider in the algebra S the chain of subspaces
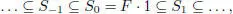
where Sr = (0) for r < 0, 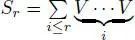 for r ≥ 1. Clearly,
for r ≥ 1. Clearly, 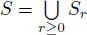 .
.
THEOREM 1.10 (Martin and Piard (1992)).–
1 1) For every r ≥ 1, Sr/Sr–2 is a unital irreducible Jordan bimodule over J.
2 2) Let V′= Fu ⊕ V, where |u| = 0. Extend the bilinear form 〈 , 〉 to V′ via 〈u, u〉 = 1, 〈u, V〉 = (0). Then for every even r ≥ 0, the quotient uSr /uSr–2 is a unital irreducible Jordan bimodule over J.
3 3) Every unital irreducible finite dimensional J-bimodule is isomorphic to Sr/Sr–2 or to uSr/uSr–2 for even r.
The classification of irreducible Jordan bimodules over M 1+1( F ) (+), D ( t ), K 3, JP(2) is too technical for an Encyclopedia survey. For a detailed description of finite dimensional irreducible Jordan bimodules, (see Martínez and Zelmanov (2003), Martin and Piard (1992), Martínez and Zelmanov (2006), Martínez and Shestakov (2020)). We will make only some general comments.
Читать дальше

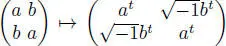 is a pseudoinvolution on Q ( n ).
is a pseudoinvolution on Q ( n ).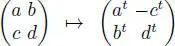 is a pseudoinvolution on Mm+n ( F ).
is a pseudoinvolution on Mm+n ( F ).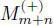 , m + n ≥ 3 or Q ( n ) (+), n ≥ 3, is one of examples 1.27and 1.28with an involution or a pseudoinvolution, or a regular bimodule.
, m + n ≥ 3 or Q ( n ) (+), n ≥ 3, is one of examples 1.27and 1.28with an involution or a pseudoinvolution, or a regular bimodule.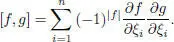
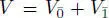 be a ℤ/2ℤ-graded vector space with a non-degenerate supersymmetric bilinear form. Assume
be a ℤ/2ℤ-graded vector space with a non-degenerate supersymmetric bilinear form. Assume 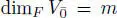 ,
, 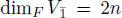 and choose a basis e 1,…, em in
and choose a basis e 1,…, em in 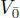 with 〈 ei , ej 〉 = δij and a basis v 1, w 1,…, vn , wn in
with 〈 ei , ej 〉 = δij and a basis v 1, w 1,…, vn , wn in 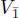 such that
such that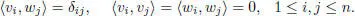
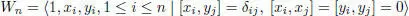
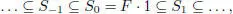
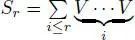 for r ≥ 1. Clearly,
for r ≥ 1. Clearly, 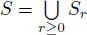 .
.










