THEOREM 1.5 (Zelmanov (2000)).– Let J be a finite dimensional Jordan superalgebra. Then J is semisimple if and only if
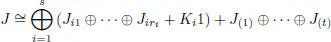
where J (1),…, J (t)are simple Jordan superalgebras and for every i = 1,…, s , the superalgebras Jij are simple non-unital Jordan superalgebras over the field extension Ki of F .
1.7. Finite dimensional representations
Jacobson (1968) developed the theory of bimodules over semisimple finite dimensional Jordan algebras.
In this section, we discuss representations (bimodules) of finite dimensional Jordan superalgebras.
DEFINITION 1.15.– The rank of a Jordan superalgebra J is the maximal number of pairwise orthogonal idempotents in the even part .
Unless otherwise stated we will assume char F = 0.
DEFINITION 1.16.– Let V be a ℤ/2ℤ- graded vector space with bilinear mappings V × J → V , J × V → V . We call V a Jordan bimodule if the split null extension V + J is a Jordan superalgebra.
Recall that in the split null extension the multiplication extends the multiplication on J , products V ∙ J and J ∙ V are defined via the bilinear mappings above and V ∙ V = (0).
Let 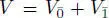 be a Jordan bimodule over J . Consider the vector space
be a Jordan bimodule over J . Consider the vector space 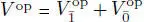 , where
, where 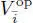 is a copy of
is a copy of 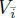 with different parity. Define the action of J on V opvia
with different parity. Define the action of J on V opvia
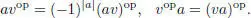
Then V opis also a Jordan bimodule over J . We call it the opposite module of V .
Let V be the free Jordan J -bimodule on one free generator.
DEFINITION 1.17.– The associative subsuperalgebra U ( J ) of End F V generated by all linear transformations RV ( a ) : V → V, v ↦ va, a ∈ J, is called the universal multiplicative enveloping superalgebra of J .
Every Jordan bimodule over J is a right module over U ( J ).
DEFINITION 1.18.– A bimodule V over J is called a one-sided bimodule if { J , V , J } = (0).
Let V ( 1/2 ) be the free one-sided Jordan J -bimodule on one free generator.
DEFINITION 1.19.– The associative subsuperalgebra S ( J ) of End F V (1/2) generated by all linear transformations RV (1/2)( a ) : V (1/2) → V (1/2), v ↦ va, a ∈ J, is called the universal associative enveloping algebra of J .
Every one-sided Jordan J-bimodule is a right module over S ( J ).
Finally, let J be a unital Jordan superalgebra with the identity element e. Let V (1) denote the free unital J-bimodule on one free generator. The associative subsuperalgebra U 1( J ) of End FV (1) generated by { RV (1/2)( a )} a ∈ J is called the universal unital enveloping algebra of J .
For an arbitrary Jordan bimodule V , the Peirce decomposition
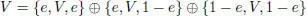
is a decomposition of V into a direct sum of unital and one-sided bimodules. Hence U ( J ) ≅ U 1( J ) ⊕ S ( J ).
1.7.1. Superalgebras of rank ≥ 3
In this section, we consider Jordan bimodules over finite dimensional simple Jordan superalgebras of rank ≥ 3, that is, superalgebras 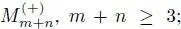 Josp( n , 2 m ), n + m ≥ 3; Q ( n ) (+), n ≥ 3; JP( n ), n ≥ 3.
Josp( n , 2 m ), n + m ≥ 3; Q ( n ) (+), n ≥ 3; JP( n ), n ≥ 3.
In this case, the universal multiplicative enveloping superalgebra U ( J ) is finite dimensional and semisimple (Martin and Piard 1992). Hence every Jordan bimodule is completely reducible, as in the case of Jordan algebras.
The superalgebras Josp( n , 2 m ) and JP( n ) are of the type
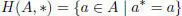
where A is a simple finite dimensional associative superalgebra and ∗ is an involution.
EXAMPLE 1.25.– An arbitrary right module over A is a one-sided module over H ( A , ∗).
EXAMPLE 1.26.– The subspace K ( A , ∗) = { k ∈ A | k ∗= – k } with the action k ∙ a = ka + ak ; k ∈ K ( A , ∗), a ∈ H ( A , ∗) is a unital H ( A , ∗)-bimodule.
THEOREM 1.6 (Martin and Piard (1992)).– An arbitrary irreducible Jordan bimodule over Josp( n , 2 m ), n + m ≥ 3, or JP( n ), n ≥ 3, is a bimodule of examples 1.25and 1.26or the regular bimodule.
The superalgebras 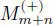 , Q ( n ) (+)are of the type A (+), where A is a simple finite dimensional associative superalgebra.
, Q ( n ) (+)are of the type A (+), where A is a simple finite dimensional associative superalgebra.
EXAMPLE 1.27.– Every right module over A gives rise to a one-sided Jordan bimodule over A (+).
Suppose now that the superalgebra A is equipped with an involution ∗.
EXAMPLE 1.28.– The subspaces H ( A , ∗) and K ( A , ∗) become Jordan A (+)- bimodules with the actions:
1 1) h ○ a = ha + a∗h;
2 2) h ○ a = ha∗ + ah;
3 3) k ○ a = ka + a∗k;
4 4) k ○ a = ka∗ + ak;
where h ∈ H ( A , ∗), k ∈ K ( A , ∗), a ∈ A .
The associative superalgebras Mm+n ( F ), where both m , n are odd, and Q ( n ), are not equipped with an involution, but they are equipped with a pseudoinvolution.
DEFINITION 1.20.– A graded linear map ∗ : A → A is called a pseudoinvolution if ( ab )∗ = (–1)| a|∙|b| b ∗ a ∗, ( a ∗)∗ = (–1) |a| a for arbitrary elements 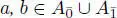 .
.
Читать дальше

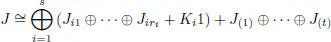
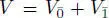 be a Jordan bimodule over J . Consider the vector space
be a Jordan bimodule over J . Consider the vector space 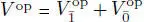 , where
, where 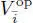 is a copy of
is a copy of 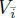 with different parity. Define the action of J on V opvia
with different parity. Define the action of J on V opvia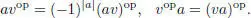
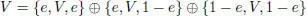
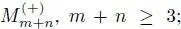 Josp( n , 2 m ), n + m ≥ 3; Q ( n ) (+), n ≥ 3; JP( n ), n ≥ 3.
Josp( n , 2 m ), n + m ≥ 3; Q ( n ) (+), n ≥ 3; JP( n ), n ≥ 3.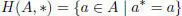
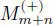 , Q ( n ) (+)are of the type A (+), where A is a simple finite dimensional associative superalgebra.
, Q ( n ) (+)are of the type A (+), where A is a simple finite dimensional associative superalgebra.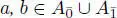 .
.










