1 ...8 9 10 12 13 14 ...26 EXAMPLE 1.32.– Let α ∈ ℂ. Then S ( n, α ) = { D ∈ W (1 : n ) | div ( tαD ) = 0} < W (1 : n ). Here if
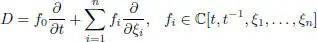
then
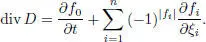
If α ∈ ℤ, then [ S ( n , α ), S ( n , α )] is a proper ideal in S ( n , α ) and the superalgebra [ S ( n , α ), S ( n , α )] is simple. This family of superalgebras appeared in physics literature (Ademollo et al . 1976; Schwimmer and Seiberg 1987) under the name “ SU2 -superconformal algebras”.
EXAMPLE 1.33.– Consider the associative commutative superalgebra
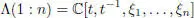
and the contact bracket [ , ] of example 1.19. The superalgebra K ( n ) = (Λ(1 : n ), [ , ]) is simple unless n = 4. For n = 4, the commutator ideal [ K (4), K (4)] has codimension 1 and [ K (4), K (4)] is a simple superalgebra. This series is known in physics literature as “ SOn -superconformal algebras” (Ademollo et al . 1976; Schoutens 1987).
EXAMPLE 1.34.– In section 1.5, for an arbitrary associative commutative algebra Z with a derivation d : Z → Z , we constructed the Jordan superalgebra JCK( Z , d ). The Lie superalgebra CK( Z , d ) is the Tits–Kantor–Koecher construction of JCK ( Z , d ). Taking Z = ℂ[ t , t –1] and 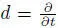 or
or 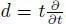 , we get the Cheng–Kac superalgebras CK(6) discovered by Cheng and Kac (1997) and independently by Grozman et al . (2001).
, we get the Cheng–Kac superalgebras CK(6) discovered by Cheng and Kac (1997) and independently by Grozman et al . (2001).
Kac and van de Leur (1989) conjectured that examples 1.31– 1.34exhaust all superconformal algebras.
The superalgebras K ( n ) and CK(6) appear as Tits–Kantor–Koecher constructions of Jordan superalgebras.
Let [ , ] be the Jordan bracket on Λ(1 : n ) = ℂ [ t , t –1, ξ 1,…, ξn ] of example 1.20, Jn = K (Λ(1 : n ), [ , ]) is the Kantor double of this bracket. Then
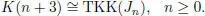
In Kac et al . (2001), we classified “superconformal” Jordan superalgebras.
THEOREM 1.11 (Kac et al . (2001)).– Let 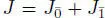 be a ℤ-graded Jordan superalgebra that is graded simple and the dimensions of all homogeneous components dim Ji , i ∈ ℤ are uniformly bounded. Then either
be a ℤ-graded Jordan superalgebra that is graded simple and the dimensions of all homogeneous components dim Ji , i ∈ ℤ are uniformly bounded. Then either
1 1) J has finitely many negative (respectively, positive) non-zero homogeneous components;
2 2) or J is isomorphic to one of the superalgebras Jn, JCK(6), n ≥ 1 or a twisted version of it.
This theorem agrees with the Kac–van de Leur conjecture on classification of superconformal algebras.
Ademollo, M., Brink, L., d’Adda, A., d’Auria, R., Napolitano, E., Scinto, S., Del Giudice, E., Di Vecchia, P., Ferrera, S., Gliozzi, F., Musto, R., Pettorino, R. (1976). Supersymmetric strings and color confinement. Phys. Lett ., 62B, 105–110.
Benkart, G., Elduque, A. (2002). A new construction of the Kac Jordan superalgebra. Proc. Amer. Math. Soc ., 130(11), 3209–3217.
Cantarini, N., Kac, V.G. (2007). Classification of linearly compact simple Jordan and generalized Poisson superalgebras. J. Algebra , 313(1), 100–124.
Cheng, S.-J., Kac, V.G. (1997). A new N = 6 superconformal algebra. Comm. Math. Phys ., 186(1), 219–231.
Grozman, P., Leites, D., Shchepochkina, I. (2001). Lie superalgebras of string theories. Acta Math. Vietnam ., 26(1), 27–63.
Jacobson, N. (1968). Structure and Representations of Jordan Algebras . American Mathematical Society Colloquium Publications, American Mathematical Society, Providence.
Kac, V.G. (1977a). Classification of simple Z -graded Lie superalgebras and simple Jordan superalgebras. Comm. Algebra , 5(13), 1375–1400.
Kac, V.G. (1977b). Lie superalgebras. Adv. Math ., 26(1), 8–96.
Kac, V.G., Martinez, C., Zelmanov, E. (2001). Graded simple Jordan superalgebras of growth one. Mem. Amer. Math. Soc ., 150(711).
Kac, V.G., van de Leur, J.W. (1989). On classification of superconformal algebras. In Strings ‘88 ( College Park, MD ). World Science Publishing, Teaneck, 77–106.
Kantor, I.L. (1972). Certain generalizations of Jordan algebras. Trudy Sem. Vektor. Tenzor. Anal ., 16, 407–499.
Kantor, I.L. (1990). Connection between Poisson brackets and Jordan and Lie superalgebras. In Lie Theory, Differential Equations and Representation Theory, Montreal , PQ, 1989 . University of Montréal, Montreal, 213–225.
Kashuba, I., Serganova, V. (2020). Representations of simple Jordan superalgebras. Adv. Math ., 370.
King, D., McCrimmon, K. (1992). The Kantor construction of Jordan superalgebras. Comm. Algebra , 20(1), 109–126.
Koecher, M. (1967). Imbedding of Jordan algebras into Lie algebras. I. Amer. J. Math ., 89, 787–816.
Martin, C., Piard, A. (1992). Classification of the indecomposable bounded admissible modules over the virasoro Lie algebra with weightspaces of dimension not exceeding two. Comm. Math. Phys ., 150(3), 465–493.
Martínez, C., Shestakov, I. (2020). Jordan bimodules over the superalgebra M 1+1. Glasgow Math. J ., 62(3). [Online].
Martínez, C., Shestakov, I., Zelmanov, E. (2001). Jordan superalgebras defined by brackets. J. London Math. Soc ., 64(2), 357–368.
Martínez, C., Shestakov, I., Zelmanov, E. (2010). Jordan bimodules over the superalgebras P ( n ) and Q ( n ). Trans. Amer. Math. Soc ., 362(4), 2037–2051.
Martinez, C., Zelmanov, E. (2001). Simple finite-dimensional Jordan superalgebras of prime characteristic. J. Algebra . 236(2), 575–629.
Martínez, C., Zelmanov, E. (2006). Unital bimodules over the simple Jordan superalgebra D ( t ). Trans. Amer. Math. Soc ., 358(8), 3637–3649.
Martínez, C., Zelmanov, E. (2009). Jordan superalgebras and their representations. In Algebras, Representations and Applications . Futorney, V., Kac, V., Kashuba, I., Zelmanov, E. (eds). American Mathematical Society , Providence, 179–194.
Martínez, C., Zelmanov, E. (2010). Representation theory of Jordan superalgebras. I. Trans. Amer. Math. Soc ., 362(2), 815–846.
Martínez, C., Zelmanov, E. (2014). Irreducible representations of the exceptional Cheng-Kac superalgebra. Trans. Amer. Math. Soc ., 366(11), 5853–5876.
Читать дальше

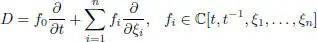
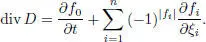
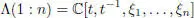
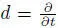 or
or 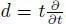 , we get the Cheng–Kac superalgebras CK(6) discovered by Cheng and Kac (1997) and independently by Grozman et al . (2001).
, we get the Cheng–Kac superalgebras CK(6) discovered by Cheng and Kac (1997) and independently by Grozman et al . (2001).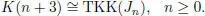
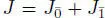 be a ℤ-graded Jordan superalgebra that is graded simple and the dimensions of all homogeneous components dim Ji , i ∈ ℤ are uniformly bounded. Then either
be a ℤ-graded Jordan superalgebra that is graded simple and the dimensions of all homogeneous components dim Ji , i ∈ ℤ are uniformly bounded. Then either










