Given a norm 1 quaternion q , there is an angle α ∈ [0, π ] and a norm 1 imaginary quaternion u such that q = (cos α )1 + (sin α ) u .
Consider the linear map:
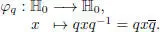
Complete u to an orthonormal basis { u , v , u × v }. A simple computation gives:
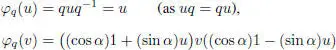
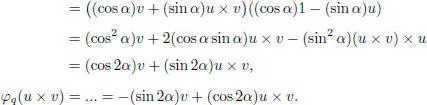
Thus, the coordinate matrix of φq relative to the basis { u , v , u × v } is
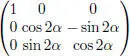
In other words, φq is a rotation around the semi-axis ℝ + u of angle 2 α , and hence the map
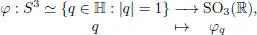
is a surjective (Lie) group homomorphism with ker φ = {±1}. We thus obtain the isomorphism
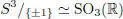
Actually, the group S 3is the universal cover of SO 3(ℝ).
Therefore, we get that rotations can be identified with conjugation by norm 1 quaternions modulo ±1. The outcome is that it is quite easy now to compose rotations in three-dimensional Euclidean space, as it is enough to multiply norm 1 quaternions: φp φq = φpq . From this, one can very easily deduce the 1840 formulas by Olinde Rodrigues (Rodrigues 1840) for the composition of rotations.
But there is more about rotations and quaternions.
For any p ∈ ℍ with n ( p ) = 1, the left (respectively, right) multiplication Lp (respectively, Rp ) by p is an isometry, due to the multiplicativity of the norm. Using [2.2], it follows that the characteristic polynomial of Lp and Rp is x 2− tr( p ) x + 1) 2and, in particular, the determinant of the multiplication by p is 1, so both Lp and Rp are rotations.
Now, if ψ is a rotation in ℝ 4≃ ℍ, a = ψ (1) is a norm 1 quaternion, and
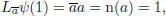
so the composition 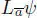 is actually a rotation in ℝ 3≃ ℍ 0. Hence, there is a norm 1 quaternion q ∈ ℍ such that
is actually a rotation in ℝ 3≃ ℍ 0. Hence, there is a norm 1 quaternion q ∈ ℍ such that
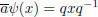
for any x ∈ ℍ. That is, for any x ∈ ℍ,
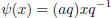
It follows that the map
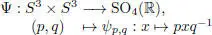
is a surjective (Lie) group homomorphism with ker Ψ = {±(1, 1)}. We thus obtain the isomorphism
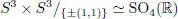
and from here we get the isomorphism SO 3(ℝ) × SO 3(ℝ) ≃ PSO 4(ℝ).
Again, this means that it is easy to compose rotations in four-dimensional space, as it reduces to multiplying pairs of norm 1 quaternions: ψp 1, q1 ψp 2, q2= ψp 1p2, q1q2.
In a letter from Graves to Hamilton, dated October 26, 1843, only a few days after the “discovery” of quaternions, Graves writes:
There is still something in the system which gravels me. I have not yet any clear views as to the extent to which we are at liberty arbitrarily to create imaginaries, and to endow them with supernatural properties.
If with your alchemy you can make three pounds of gold, why should you stop there?
Actually, as we have seen in [2.3], the algebra of quaternions is obtained by doubling suitably the field of complex numbers: ℍ = ℂ ⊕ ℂ j.
Doubling again we get the octonions (Graves–Cayley):
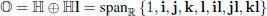
with multiplication mimicked from [2.2]:
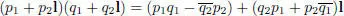
and usual norm: n( p 1+ p 2 l) = n( p 1) + n ( p 2), for p 1, p 2, q 1, q 2∈ ℍ.
This was already known to Graves, who wrote a letter to Hamilton on December 26, 1843 with his discovery of what he called octaves . Hamilton promised to announce Graves’ discovery to the Irish Royal Academy, but did not do it in time. In 1845, independently, Cayley discovered the octonions and got the credit. Octonions are also called Cayley numbers .
Some properties of this new algebra of octonions are summarized here:
– The norm is multiplicative: n(xy) = n(x)n(y), for any .
– is a division algebra, and it is neither commutative nor associative!
But it is alternative , that is, any two elements generate an associative subalgebra.
A theorem by Zorn (1933) asserts that the only finite-dimensional real alternative division algebras are ℝ, ℂ, ℍ and 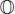 . And hence, as proved by Frobenius (1878), the only such associative algebras are ℝ, ℂ and ℍ.
. And hence, as proved by Frobenius (1878), the only such associative algebras are ℝ, ℂ and ℍ.
– The seven-dimensional Euclidean sphere is not a group (associativity fails), but it constitutes the most important example of a Moufang loop.
– As for ℍ, for any two imaginary octonions u, we have:

for the usual scalar product u ∙ v on 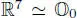 , and where u × v defines the usual cross-product in ℝ 7. This satisfies the identity ( u × v ) × v = ( u ∙ v ) v − ( v ∙ v ) u , for any u , v ∈ ℝ 7.
, and where u × v defines the usual cross-product in ℝ 7. This satisfies the identity ( u × v ) × v = ( u ∙ v ) v − ( v ∙ v ) u , for any u , v ∈ ℝ 7.
– is again a quadratic algebra: x2 − tr(x)x + n(x)1 = 0 for any , where and , where for x = a1 + u, a ∈ ℝ, , .
Читать дальше

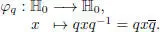
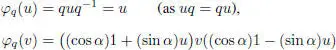
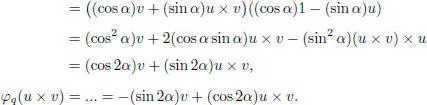
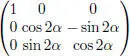
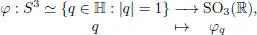
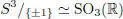
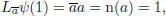
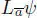 is actually a rotation in ℝ 3≃ ℍ 0. Hence, there is a norm 1 quaternion q ∈ ℍ such that
is actually a rotation in ℝ 3≃ ℍ 0. Hence, there is a norm 1 quaternion q ∈ ℍ such that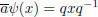
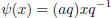
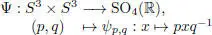
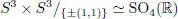
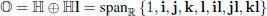
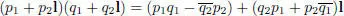
 . And hence, as proved by Frobenius (1878), the only such associative algebras are ℝ, ℂ and ℍ.
. And hence, as proved by Frobenius (1878), the only such associative algebras are ℝ, ℂ and ℍ.
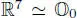 , and where u × v defines the usual cross-product in ℝ 7. This satisfies the identity ( u × v ) × v = ( u ∙ v ) v − ( v ∙ v ) u , for any u , v ∈ ℝ 7.
, and where u × v defines the usual cross-product in ℝ 7. This satisfies the identity ( u × v ) × v = ( u ∙ v ) v − ( v ∙ v ) u , for any u , v ∈ ℝ 7.










