The non-degeneracy of the restriction of n to  implies that
implies that  is associative. In particular, any proper subalgebra of
is associative. In particular, any proper subalgebra of  with non-degenerate restricted norm is associative.
with non-degenerate restricted norm is associative.
Conversely, given an associative Hurwitz algebra  with non-degenerate n, and a non-zero scalar
with non-degenerate n, and a non-zero scalar 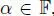 , consider the direct sum of two copies of
, consider the direct sum of two copies of  , with multiplication and norm given by [2.7], extending those on
, with multiplication and norm given by [2.7], extending those on  . The arguments above show that (
. The arguments above show that (  , ∙, n) is again a Hurwitz algebra, which is said to be obtained by the Cayley–Dickson doubling process from (
, ∙, n) is again a Hurwitz algebra, which is said to be obtained by the Cayley–Dickson doubling process from (  , ∙, n) and α . This algebra is denoted by
, ∙, n) and α . This algebra is denoted by 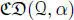 .
.
REMARK 2.1.– 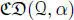 is associative if and only if
is associative if and only if  is commutative. This follows from x ∙ ( y ∙ u ) = ( y ∙ x ) ∙ u . If the algebra is associative, this equals ( x ∙ y ) ∙ u , and it forces x ∙ y = y ∙ x for any x ,
is commutative. This follows from x ∙ ( y ∙ u ) = ( y ∙ x ) ∙ u . If the algebra is associative, this equals ( x ∙ y ) ∙ u , and it forces x ∙ y = y ∙ x for any x , 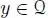 . The converse is an easy exercise.
. The converse is an easy exercise.
We arrive at the main result of this section.
THEOREM 2.1 (Generalized Hurwitz theorem).– Every Hurwitz algebra over a field  is isomorphic to one of the following:
is isomorphic to one of the following:
1 1) the ground field ;
2 2) a two-dimensional separable commutative and associative algebra: , with v∙2 = v + μ1, with 4μ +1 ≠ 0, and n(∊ + δv) = ∊2 − μδ2 + ∊δ, for ∊, ;
3 3) a quaternion algebra for as in (2) and ;
4 4) a Cayley (or octonion) algebra , for as in (3) and .
In particular, the dimension of a Hurwitz algebra is restricted to 1, 2, 4 or 8.
PROOF.– The only Hurwitz algebra of dimension 1 is, up to isomorphism, the ground field. If (  , ∙, n) is a Hurwitz algebra and
, ∙, n) is a Hurwitz algebra and 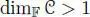 , there is an element
, there is an element 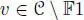 such that n( v , 1) = 1 and
such that n( v , 1) = 1 and 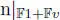 is non-degenerate. The Cayley–Hamilton equation shows that v ∙2− v + n( v )1= 0, so v ∙2= v + μ 1, with μ = −n( v ). The non-degeneracy condition is equivalent to the condition 4 μ + 1 ≠ 0. Then
is non-degenerate. The Cayley–Hamilton equation shows that v ∙2− v + n( v )1= 0, so v ∙2= v + μ 1, with μ = −n( v ). The non-degeneracy condition is equivalent to the condition 4 μ + 1 ≠ 0. Then 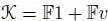 is a Hurwitz subalgebra of
is a Hurwitz subalgebra of  and, if
and, if 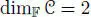 , we are done.
, we are done.
If  , we may take an element
, we may take an element 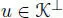 with n( u ) = − β ≠ 0, and hence the subspace
with n( u ) = − β ≠ 0, and hence the subspace 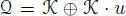 is a subalgebra of
is a subalgebra of  isomorphic to
isomorphic to 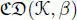 . By the previous remark,
. By the previous remark,  is associative (as
is associative (as  is commutative), but it fails to be commutative, as
is commutative), but it fails to be commutative, as 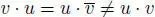 . If
. If 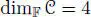 , we are done.
, we are done.
Finally, if 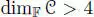 , we may take an element
, we may take an element 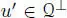 with n( u ʹ) = − γ ≠ 0, and hence the subspace
with n( u ʹ) = − γ ≠ 0, and hence the subspace 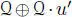 is a subalgebra of
is a subalgebra of  isomorphic to
isomorphic to 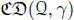 , which is not associative by remark 2.1, so it is necessarily the whole
, which is not associative by remark 2.1, so it is necessarily the whole  . □
. □
Note that if char 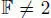 , the restriction of n to
, the restriction of n to 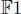 is non-degenerate, so we could have used the same argument for dimension > 1 in the proof above than the one used for
is non-degenerate, so we could have used the same argument for dimension > 1 in the proof above than the one used for  > 2. Hence, we get:
> 2. Hence, we get:
Читать дальше

 implies that
implies that  with non-degenerate restricted norm is associative.
with non-degenerate restricted norm is associative.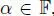 , consider the direct sum of two copies of
, consider the direct sum of two copies of  , with multiplication and norm given by [2.7], extending those on
, with multiplication and norm given by [2.7], extending those on 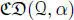 .
.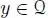 . The converse is an easy exercise.
. The converse is an easy exercise. is isomorphic to one of the following:
is isomorphic to one of the following: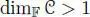 , there is an element
, there is an element 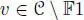 such that n( v , 1) = 1 and
such that n( v , 1) = 1 and 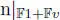 is non-degenerate. The Cayley–Hamilton equation shows that v ∙2− v + n( v )1= 0, so v ∙2= v + μ 1, with μ = −n( v ). The non-degeneracy condition is equivalent to the condition 4 μ + 1 ≠ 0. Then
is non-degenerate. The Cayley–Hamilton equation shows that v ∙2− v + n( v )1= 0, so v ∙2= v + μ 1, with μ = −n( v ). The non-degeneracy condition is equivalent to the condition 4 μ + 1 ≠ 0. Then 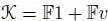 is a Hurwitz subalgebra of
is a Hurwitz subalgebra of 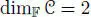 , we are done.
, we are done. , we may take an element
, we may take an element 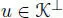 with n( u ) = − β ≠ 0, and hence the subspace
with n( u ) = − β ≠ 0, and hence the subspace 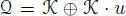 is a subalgebra of
is a subalgebra of 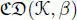 . By the previous remark,
. By the previous remark,  is commutative), but it fails to be commutative, as
is commutative), but it fails to be commutative, as 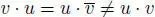 . If
. If 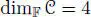 , we are done.
, we are done.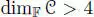 , we may take an element
, we may take an element 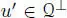 with n( u ʹ) = − γ ≠ 0, and hence the subspace
with n( u ʹ) = − γ ≠ 0, and hence the subspace 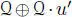 is a subalgebra of
is a subalgebra of 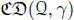 , which is not associative by remark 2.1, so it is necessarily the whole
, which is not associative by remark 2.1, so it is necessarily the whole 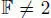 , the restriction of n to
, the restriction of n to 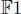 is non-degenerate, so we could have used the same argument for dimension > 1 in the proof above than the one used for
is non-degenerate, so we could have used the same argument for dimension > 1 in the proof above than the one used for 










