COROLLARY 2.1.– Every Hurwitz algebra over a field  of characteristic not 2 is isomorphic to one of the following:
of characteristic not 2 is isomorphic to one of the following:
1 1) the ground field ;
2 2) a two-dimensional algebra for a non-zero scalar α;
3 3) a quaternion algebra for as in (2) and ;
4 4) a Cayley (or octonion) algebra , for as in (3) and .
REMARK 2.2.– Over the real field ℝ, the scalars α , β and γ in corollary 2.1 can be taken to be ±1. Note that [2.3]and the analogous equation for ℂ and 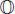 give isomorphisms
give isomorphisms 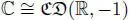 ,
, 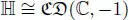 and
and 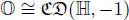 .
.
REMARK 2.3.– Hurwitz (1898) only considered the real case with a positive definite norm. Over the years, this was extended in several ways. The actual version of the generalized Hurwitz theorem seems to appear for the first time in Jacobson (1958) (if char 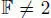 ) and van der Blij and Springer (1959).
) and van der Blij and Springer (1959).
The problem of isomorphism between Hurwitz algebras of the same dimension relies on the norms:
PROPOSITION 2.3.– Two Hurwitz algebras over a field are isomorphic if and only if their norms are isometric.
PROOF.– Any isomorphism of Hurwitz algebras is, in particular, an isometry of the corresponding norms, due to the Cayley–Hamilton equation. The converse follows from Witt’s cancellation theorem (see Elman et al . (2008, theorem 8.4)). □
A natural question is whether the restriction of the dimension of a Hurwitz algebra to be 1, 2, 4 or 8 is still valid for arbitrary composition algebras. The answer is that this is the case for finite-dimensional composition algebras.
COROLLARY 2.2.– Let (  , ∙, n) be a finite-dimensional composition algebra. Then its dimension is either 1, 2, 4 or 8.
, ∙, n) be a finite-dimensional composition algebra. Then its dimension is either 1, 2, 4 or 8.
PROOF.– Let 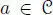 be an element of non-zero norm. Then
be an element of non-zero norm. Then 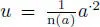 satisfies n( u ) = 1. Using the so-called Kaplansky’s trick (Kaplansky 1953), consider the new multiplication
satisfies n( u ) = 1. Using the so-called Kaplansky’s trick (Kaplansky 1953), consider the new multiplication
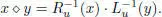
Note that since the left and right multiplications by a norm 1 element are isometries, we still have n( x ◊ y ) = n( x )n( y ), so (  , ◊, n) is a composition algebra too. But
, ◊, n) is a composition algebra too. But 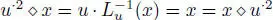 for any x , so the element u ∙2is the unity of (
for any x , so the element u ∙2is the unity of (  , ◊) and (
, ◊) and (  , ◊, n) is a Hurwitz algebra, and hence
, ◊, n) is a Hurwitz algebra, and hence 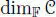 is restricted to 1, 2, 4. or 8. □
is restricted to 1, 2, 4. or 8. □
However, contrary to the thoughts expressed in Kaplansky (1953), there are examples of infinite-dimensional composition algebras. For example (see Urbanik and Wright (1960)), let φ : ℕ × ℕ → ℕ be a bijection (for instance, φ ( n , m ) = 2 n−1(2 m − 1)), and let  be a vector space over a field
be a vector space over a field  of characteristic not 2 with a countable basis { un : n ∈ ℕ}. Define a multiplication and a norm on
of characteristic not 2 with a countable basis { un : n ∈ ℕ}. Define a multiplication and a norm on  by
by

Then ( 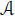 , ∙, n) is a composition algebra.
, ∙, n) is a composition algebra.
In Elduque and Pérez (1997), one may find examples of infinite-dimensional composition algebras of arbitrary infinite dimension, which are even left unital.
2.3.2. Isotropic Hurwitz algebras
Assume now that the norm of a Hurwitz algebra (  , ∙, n) represents 0. That is, there is a non-zero element
, ∙, n) represents 0. That is, there is a non-zero element 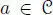 such that n( a ) = 0. This is always the case if
such that n( a ) = 0. This is always the case if 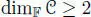 and
and  is algebraically closed.
is algebraically closed.
With a as above, take  such that
such that 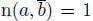 , so that n( a ∙ b , 1) = 1. Also n( a ∙ b ) = n( a )n( b ) = 0. By the Cayley–Hamilton equation, the non-zero element e 1:= a ∙ b satisfies
, so that n( a ∙ b , 1) = 1. Also n( a ∙ b ) = n( a )n( b ) = 0. By the Cayley–Hamilton equation, the non-zero element e 1:= a ∙ b satisfies 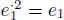 , that is, e 1is an idempotent. Consider too the idempotent
, that is, e 1is an idempotent. Consider too the idempotent  , and the subalgebra
, and the subalgebra 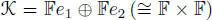 generated by e 1. (1= e 1+ e 2).
generated by e 1. (1= e 1+ e 2).
Читать дальше

 of characteristic not 2 is isomorphic to one of the following:
of characteristic not 2 is isomorphic to one of the following: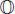 give isomorphisms
give isomorphisms 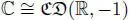 ,
, 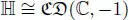 and
and 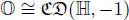 .
.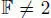 ) and van der Blij and Springer (1959).
) and van der Blij and Springer (1959). , ∙, n) be a finite-dimensional composition algebra. Then its dimension is either 1, 2, 4 or 8.
, ∙, n) be a finite-dimensional composition algebra. Then its dimension is either 1, 2, 4 or 8.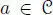 be an element of non-zero norm. Then
be an element of non-zero norm. Then 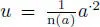 satisfies n( u ) = 1. Using the so-called Kaplansky’s trick (Kaplansky 1953), consider the new multiplication
satisfies n( u ) = 1. Using the so-called Kaplansky’s trick (Kaplansky 1953), consider the new multiplication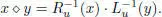
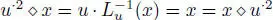 for any x , so the element u ∙2is the unity of (
for any x , so the element u ∙2is the unity of (  is restricted to 1, 2, 4. or 8. □
is restricted to 1, 2, 4. or 8. □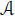 be a vector space over a field
be a vector space over a field 
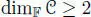 and
and  such that
such that 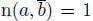 , so that n( a ∙ b , 1) = 1. Also n( a ∙ b ) = n( a )n( b ) = 0. By the Cayley–Hamilton equation, the non-zero element e 1:= a ∙ b satisfies
, so that n( a ∙ b , 1) = 1. Also n( a ∙ b ) = n( a )n( b ) = 0. By the Cayley–Hamilton equation, the non-zero element e 1:= a ∙ b satisfies 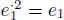 , that is, e 1is an idempotent. Consider too the idempotent
, that is, e 1is an idempotent. Consider too the idempotent  , and the subalgebra
, and the subalgebra 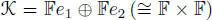 generated by e 1. (1= e 1+ e 2).
generated by e 1. (1= e 1+ e 2).










