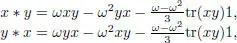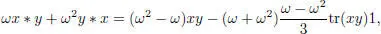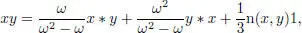EXAMPLES 2.1(Okubo (1978)).–
– Para-Hurwitz algebras: let (, ∙, n) be a Hurwitz algebra and consider the composition algebra (, ∙, n) with the new product given by
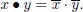
Then 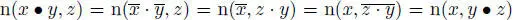 , for any x , y , z , so that (
, for any x , y , z , so that (  , ∙, n ) is a symmetric composition algebra (note that
, ∙, n ) is a symmetric composition algebra (note that  for any x : 1 is a para-unit of (
for any x : 1 is a para-unit of (  , ∙, n)).
, ∙, n)).
– Okubo algebras: assume char (the case of char requires a different definition), and let be a primitive cubic root of 1. Let be a central simple associative algebra of degree 3 with trace tr, and let . For any , the quadratic form make sense even if char (check this!). Now define a multiplication and norm on by:
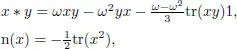
Then, for any x , 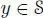 :
:
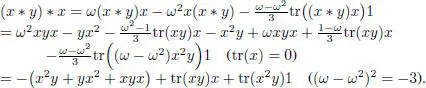
But if tr( x ) = 0, then 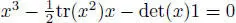 , so
, so
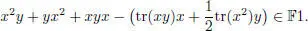
Since  , we have
, we have  .
.
Therefore, (  , ∗, n) is a symmetric composition algebra.
, ∗, n) is a symmetric composition algebra.
In case 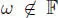 , take
, take 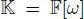 and a central simple associative algebra
and a central simple associative algebra 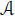 of degree 3 over
of degree 3 over 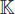 endowed with a
endowed with a 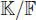 -involution of second kind J. Then take
-involution of second kind J. Then take 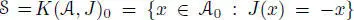 (this is an
(this is an  -subspace) and use the same formulas above to define the multiplication and the norm.
-subspace) and use the same formulas above to define the multiplication and the norm.
REMARK 2.5.– For 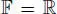 , take
, take 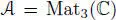 , and then there appears the Okubo algebra (
, and then there appears the Okubo algebra (  , ∗, n) with
, ∗, n) with 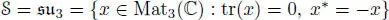 ( x ∗ denotes the conjugate transpose of x ). This algebra was termed the algebra of pseudo-octonions by Okubo (1978), who studied these algebras and classified them, under some restrictions, in joint work with Osborn Okubo and Osborn (1981a,b).
( x ∗ denotes the conjugate transpose of x ). This algebra was termed the algebra of pseudo-octonions by Okubo (1978), who studied these algebras and classified them, under some restrictions, in joint work with Osborn Okubo and Osborn (1981a,b).
The name Okubo algebras was given in Elduque and Myung (1990). Faulkner (1988) discovered Okubo’s construction independently, in a more general setting, related to separable alternative algebras of degree 3, and gave the key idea for the classification of the symmetric composition algebras in Elduque and Myung (1993) (char 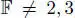 ). A different, less elegant, classification was given in Elduque and Myung (1991), based on the fact that Okubo algebras are Lie-admissible .
). A different, less elegant, classification was given in Elduque and Myung (1991), based on the fact that Okubo algebras are Lie-admissible .
The term symmetric composition algebra was given in Knus et al . (1998, Chapter VIII).
REMARK 2.6.– Given an Okubo algebra, note that for any x , 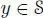 ,
,
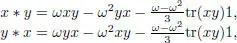
so that
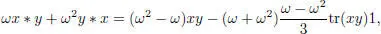
and
[2.8] 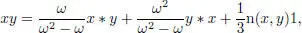
so the product in 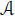 is determined by the product in the Okubo algebra.
is determined by the product in the Okubo algebra.
Also, as noted by Faulkner, the construction above is valid for separable alternative algebras of degree 3.
THEOREM 2.4 (Elduque and Myung (1991, 1993)).– Let  be a field of characteristic not 3.
be a field of characteristic not 3.
– If contains a primitive cubic root ω of 1, then the symmetric composition algebras of dimension ≥ 2 are, up to isomorphism, the algebras (, ∗, n) for a separable alternative algebra of degree 3.
Two such symmetric composition algebras are isomorphic if and only if the corresponding alternative algebras are too.
– If does not contain primitive cubic roots of 1, then the symmetric composition algebras of dimension ≥ 2 are, up to isomorphism, the algebras (K(, J)0, ∗, n) for a separable alternative algebra of degree 3 over , and J a -involution of the second kind.
Читать дальше

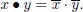
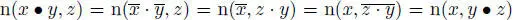 , for any x , y , z , so that (
, for any x , y , z , so that (  , ∙, n ) is a symmetric composition algebra (note that
, ∙, n ) is a symmetric composition algebra (note that  for any x : 1 is a para-unit of (
for any x : 1 is a para-unit of ( 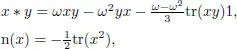
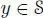 :
: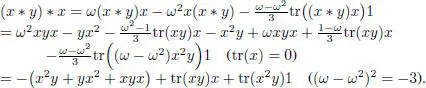
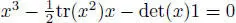 , so
, so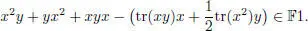
 , we have
, we have  .
. , ∗, n) is a symmetric composition algebra.
, ∗, n) is a symmetric composition algebra.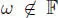 , take
, take 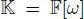 and a central simple associative algebra
and a central simple associative algebra 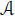 of degree 3 over
of degree 3 over 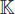 endowed with a
endowed with a 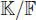 -involution of second kind J. Then take
-involution of second kind J. Then take 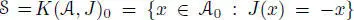 (this is an
(this is an  -subspace) and use the same formulas above to define the multiplication and the norm.
-subspace) and use the same formulas above to define the multiplication and the norm.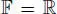 , take
, take 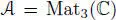 , and then there appears the Okubo algebra (
, and then there appears the Okubo algebra ( 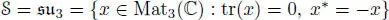 ( x ∗ denotes the conjugate transpose of x ). This algebra was termed the algebra of pseudo-octonions by Okubo (1978), who studied these algebras and classified them, under some restrictions, in joint work with Osborn Okubo and Osborn (1981a,b).
( x ∗ denotes the conjugate transpose of x ). This algebra was termed the algebra of pseudo-octonions by Okubo (1978), who studied these algebras and classified them, under some restrictions, in joint work with Osborn Okubo and Osborn (1981a,b). ). A different, less elegant, classification was given in Elduque and Myung (1991), based on the fact that Okubo algebras are Lie-admissible .
). A different, less elegant, classification was given in Elduque and Myung (1991), based on the fact that Okubo algebras are Lie-admissible .