Its twisted forms (i.e. those composition algebras (  , ∗, n) that become isomorphic to the split Okubo algebra after extending scalars to an algebraic closure) are called Okubo algebras.
, ∗, n) that become isomorphic to the split Okubo algebra after extending scalars to an algebraic closure) are called Okubo algebras.
In the basis in Figure 2.1, the multiplication table of the split Okubo algebra is given in Figure 2.2.
Over fields of characteristic ≠ 3, our new definition of Okubo algebras coincide with the definition in examples 2.1, due to corollary 2.4. Okubo and Osborn (1981b) had given an ad hoc definition of the Okubo algebra over an algebraically closed field of characteristic 3.
Note that the split Okubo algebra does not contain any non-zero element that commutes with every other element, that is, its commutative center is trivial. This is not so for the para-Hurwitz algebra, where the para-unit lies in the commutative center.
Let  be a field of characteristic 3 and let 0 ≠ α ,
be a field of characteristic 3 and let 0 ≠ α , 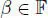 . Consider the elements
. Consider the elements

in 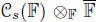 (
( 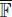 being an algebraic closure of
being an algebraic closure of  ). These elements generate, by multiplication and linear combinations over
). These elements generate, by multiplication and linear combinations over  , a twisted form of the split Okubo algebra (
, a twisted form of the split Okubo algebra ( 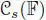 , ∗, n). Denote by
, ∗, n). Denote by  this twisted form.
this twisted form.
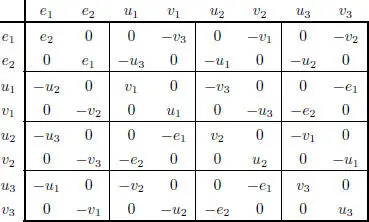
Figure 2.2. Multiplication table of the split Okubo algebra
The classification of the symmetric composition algebras in characteristic 3, which completes the classification of symmetric composition algebras over fields, is as follows (Elduque (1997), see also Chernousov et al . (2013)):
THEOREM 2.6.– Any symmetric composition algebra (  , ∗, n) over a field
, ∗, n) over a field  of characteristic 3 is either:
of characteristic 3 is either:
– a para-Hurwitz algebra. Two such algebras are isomorphic if and only if the associated Hurwitz algebras are too;
– a two-dimensional algebra with a basis {u, v} and multiplication given by
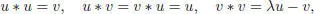
for a non-zero scalar 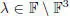 . These algebras do not contain idempotents and are twisted forms of the para-Hurwitz algebras.
. These algebras do not contain idempotents and are twisted forms of the para-Hurwitz algebras.
Algebras corresponding to the scalars λ and λʹ are isomorphic if and only if 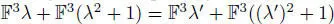 .
.
– Isomorphic to for some 0 ≠ α, . Moreover, is isomorphic or anti-isomorphic to if and only if .
A more precise statement for the isomorphism condition in the last item is given in (Elduque 1997). A key point in the proof of this theorem is the study of idempotents on Okubo algebras. If there are non-zero idempotents, then these algebras are Petersson algebras. The most difficult case appears in the absence of idempotents. This is only possible if the ground field  is not perfect.
is not perfect.
The importance of symmetric composition algebras lies in their connections with the phenomenon of triality in dimension 8, related to the fact that the Dynkin diagram D 4is the most symmetric one. The details of much of what follows can be found in (Knus et al . (1998), Chapter VIII).
Let (  , ∗, n) be an eight-dimensional symmetric composition algebra over a field
, ∗, n) be an eight-dimensional symmetric composition algebra over a field  , that is,
, that is,  is either a para-Hurwitz algebra or an Okubo algebra. Write Lx ( y ) = x ∗ y = Ry ( x ) as usual. Then, due to theorem 2.3, Lx Rx = RxLx = n( x )id for any
is either a para-Hurwitz algebra or an Okubo algebra. Write Lx ( y ) = x ∗ y = Ry ( x ) as usual. Then, due to theorem 2.3, Lx Rx = RxLx = n( x )id for any 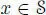 so that, inside
so that, inside 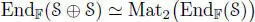 , we have
, we have
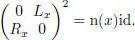
Therefore, the map
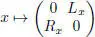
extends to an isomorphism of associative algebras with involution:

where 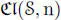 (
(  , n) is the Clifford algebra on the quadratic space (
, n) is the Clifford algebra on the quadratic space (  , n), τ is its canonical involution ( τ ( x ) = x for any
, n), τ is its canonical involution ( τ ( x ) = x for any 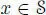 ) and σn ⊥nis the orthogonal involution on
) and σn ⊥nis the orthogonal involution on 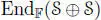 induced by the quadratic form where the two copies of S are orthogonal and the restriction on each copy coincides with the norm. The multiplication in the Clifford algebra will be denoted by juxtaposition.
induced by the quadratic form where the two copies of S are orthogonal and the restriction on each copy coincides with the norm. The multiplication in the Clifford algebra will be denoted by juxtaposition.
Читать дальше

 , ∗, n) that become isomorphic to the split Okubo algebra after extending scalars to an algebraic closure) are called Okubo algebras.
, ∗, n) that become isomorphic to the split Okubo algebra after extending scalars to an algebraic closure) are called Okubo algebras. be a field of characteristic 3 and let 0 ≠ α ,
be a field of characteristic 3 and let 0 ≠ α , 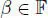 . Consider the elements
. Consider the elements
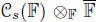 (
(  being an algebraic closure of
being an algebraic closure of  , ∗, n). Denote by
, ∗, n). Denote by  this twisted form.
this twisted form.
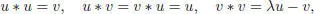
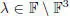 . These algebras do not contain idempotents and are twisted forms of the para-Hurwitz algebras.
. These algebras do not contain idempotents and are twisted forms of the para-Hurwitz algebras.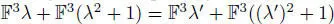 .
.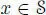 so that, inside
so that, inside 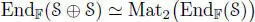 , we have
, we have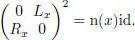
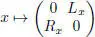

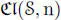 (
( 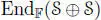 induced by the quadratic form where the two copies of S are orthogonal and the restriction on each copy coincides with the norm. The multiplication in the Clifford algebra will be denoted by juxtaposition.
induced by the quadratic form where the two copies of S are orthogonal and the restriction on each copy coincides with the norm. The multiplication in the Clifford algebra will be denoted by juxtaposition.










