Two such symmetric composition algebras are isomorphic if and only if the corresponding alternative algebras, as algebras with involution, are too.
Sketch of proof : we can go in the reverse direction of Okubo’s construction. Given a symmetric composition algebra (  , ∗, n) over a field containing ω , define the algebra
, ∗, n) over a field containing ω , define the algebra 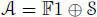 with multiplication determined by formula [2.8]. Then
with multiplication determined by formula [2.8]. Then 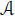 turns out to be a separable alternative algebra of degree 3.
turns out to be a separable alternative algebra of degree 3.
In case 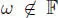 , then we must consider
, then we must consider  , with the same formula for the product. In
, with the same formula for the product. In 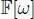 , we have the Galois automorphism ωτ = ω 2. Then the conditions J (1) = 1 and J ( s ) = − s for any
, we have the Galois automorphism ωτ = ω 2. Then the conditions J (1) = 1 and J ( s ) = − s for any 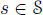 induce a
induce a 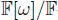 -involution of the second kind in
-involution of the second kind in 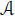 . □
. □
COROLLARY 2.4.– The algebras in examples 2.1essentially exhaust, up to isomorphism, the symmetric composition algebras over a field  of characteristic not 3.
of characteristic not 3.
Sketch of proof : let ω be a primitive cubic root of 1 in an algebraic closure of  , and let
, and let 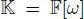 , so that
, so that 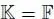 if
if 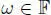 . A separable alternative algebra over
. A separable alternative algebra over 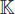 is, up to isomorphism, one of the following:
is, up to isomorphism, one of the following:
– a central simple associative algebra, and hence we obtain the Okubo algebras in examples 2.1;
– for a Hurwitz algebra , in which case (, ∗, n) is shown to be isomorphic to the para-Hurwitz algebra attached to if , and (K (K (, J)0, ∗, n) to the para-Hurwitz algebra attached to if ;
– , for a cubic field extension of (if ), in which case the symmetric composition algebra is shown to be a twisted form of a two-dimensional para-Hurwitz algebra. □
One of the clues to understand symmetric composition algebras over fields of characteristic 3 is the following result of Petersson (1969) (dealing with char 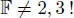 ).
).
THEOREM 2.5.– Let  be an algebraically closed field of characteristic ≠ 2, 3. Then any simple finite-dimensional algebra satisfying
be an algebraically closed field of characteristic ≠ 2, 3. Then any simple finite-dimensional algebra satisfying
[2.9] 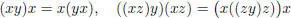
for any x , y , z is, up to isomorphism, one of the following:
– the algebra (, ∙), where (, ∙, n) is a Hurwitz algebra and (that is, a para-Hurwitz algebra);
– the algebra (, ∗), where is the split Cayley algebra, and , where φ is a precise order 3 automorphism of given, in the basis in Figure 2.1by
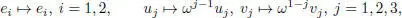
where ω is a primitive cubic root of 1.
Note that any symmetric composition algebra (  , ∗, n) satisfies [2.9]so the unique, up to isomorphism, Okubo algebra over an algebraically closed field of characteristic ≠ 2, 3 must be isomorphic to the last algebra in the theorem above, and this seems to be the first appearance of these algebras in the literature.
, ∗, n) satisfies [2.9]so the unique, up to isomorphism, Okubo algebra over an algebraically closed field of characteristic ≠ 2, 3 must be isomorphic to the last algebra in the theorem above, and this seems to be the first appearance of these algebras in the literature.
This results in the next definition:
DEFINITION 2.3 (Knus et al . (1998, §34.b)).– Let (  , ∙, n) be a Hurwitz algebra , and let φ ∈ Aut(
, ∙, n) be a Hurwitz algebra , and let φ ∈ Aut(  , ∙, n) be an automorphism with φ 3= id. The composition algebra (
, ∙, n) be an automorphism with φ 3= id. The composition algebra (  , ∗, n), with
, ∗, n), with
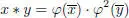
is called a Petersson algebra, and denoted by 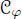 .
.
In case φ = id, the Petersson algebra is the para-Hurwitz algebra associated with (  , ∙, n).
, ∙, n).
Modifying the automorphism in theorem 2.5, consider the order 3 automorphism φ of the split Cayley algebra given by:
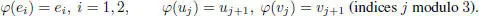
With this automorphism, we may define Okubo algebras over arbitrary fields (see Elduque and Pérez (1996)).
DEFINITION 2.4.– Let ( 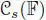 , ∙, n) be the split Cayley algebra over an arbi tr ary field
, ∙, n) be the split Cayley algebra over an arbi tr ary field  . The Petersson algebra
. The Petersson algebra  is called the split Okubo algebra over
is called the split Okubo algebra over  .
.
Читать дальше

 , ∗, n) over a field containing ω , define the algebra
, ∗, n) over a field containing ω , define the algebra 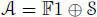 with multiplication determined by formula [2.8]. Then
with multiplication determined by formula [2.8]. Then 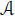 turns out to be a separable alternative algebra of degree 3.
turns out to be a separable alternative algebra of degree 3.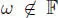 , then we must consider
, then we must consider  , with the same formula for the product. In
, with the same formula for the product. In 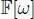 , we have the Galois automorphism ωτ = ω 2. Then the conditions J (1) = 1 and J ( s ) = − s for any
, we have the Galois automorphism ωτ = ω 2. Then the conditions J (1) = 1 and J ( s ) = − s for any 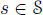 induce a
induce a 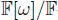 -involution of the second kind in
-involution of the second kind in  of characteristic not 3.
of characteristic not 3.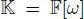 , so that
, so that 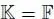 if
if 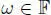 . A separable alternative algebra over
. A separable alternative algebra over 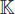 is, up to isomorphism, one of the following:
is, up to isomorphism, one of the following: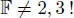 ).
).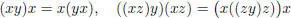
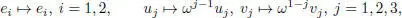
 , ∙, n) be a Hurwitz algebra , and let φ ∈ Aut(
, ∙, n) be a Hurwitz algebra , and let φ ∈ Aut( 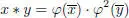
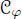 .
.
 , ∙, n) be the split Cayley algebra over an arbi tr ary field
, ∙, n) be the split Cayley algebra over an arbi tr ary field  is called the split Okubo algebra over
is called the split Okubo algebra over 










